主流框架如何定义和管理分布式张量
1. 引言
分布式张量 Dtensor(Distributed Tensor)是一个专门设计的抽象和工具,用于描述和管理分布式 Tensor 的分布式属性。DTensor 的概念由 Google 在 TensorFlow 的发展中引入,并逐步成为常见的分布式训练优化方案,也被其他框架如 PyTorch 和 Paddle 等参考和使用。
2. 分布式张量模型
在分布式训练中,描述张量如何在设备间分布是一个关键问题。主流框架都采用了一种通用的分布式张量模型,由 Mesh 和 Layout 两个核心概念组成。
2.1 Mesh:设备拓扑的逻辑表示
Mesh 是设备的一种笛卡尔拓扑表示。它将计算设备(如 GPU 或 TPU)组织成一个多维网格,用于描述设备间的逻辑关系。可以简单理解为一个设备的多维数组,每个维度称为一个 “网格维度”。
一个 Mesh 通常由以下部分构成:
- 设备列表:Mesh 包含的物理设备
- 网格维度:设备按照逻辑维度组织,例如二维网格可以表示为行和列
- 网格维度名称:每个维度可以用一个唯一的名称标识,便于分片描述
设有 8 个 GPU,编号为 0, 1, 2, 3, 4, 5, 6, 7,我们可以将其组织成一个 2x4 的二维 Mesh,如下图所示:
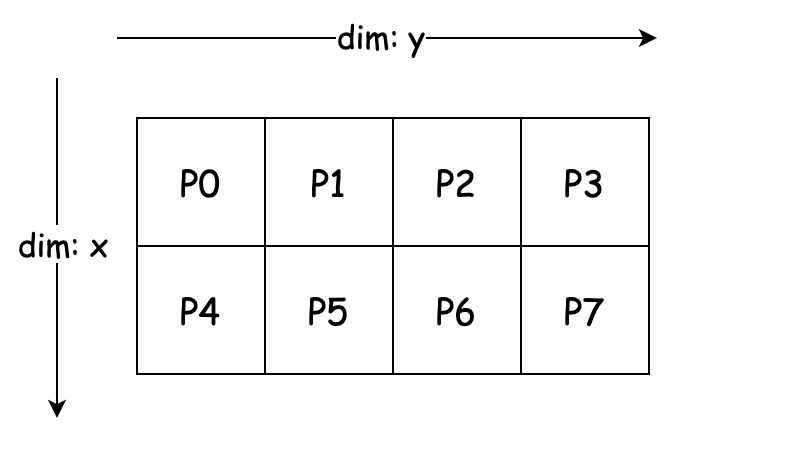
示例:2D Mesh
在实际应用过程中,我们可以在不同的 Mesh 纬度上做不同的并行化操作,比如我们可以在这个 2x4 Mesh 上实现 2D 并行,其中 数据并行的并行度为 2,张量并行的并行度为 4。
将批量数据分片到 dim: x 的 2 组设备:
- 第一组:
P0, P1, P2, P3处理第 1 个数据分片 - 第二组:
P4, P5, P6, P7处理第 2 个数据分片
将权重矩阵 W 切分到 dim: y 的 4 个设备。在每个数据并行组中,列按张量并行切分,P0 负责 W[:, 0:256],P1 负责 W[:, 256:512],依此类推。每组的设备并行计算自己的数据分片和张量分片,前向传播计算完成后,设备之间通过通信去共享中间结果。
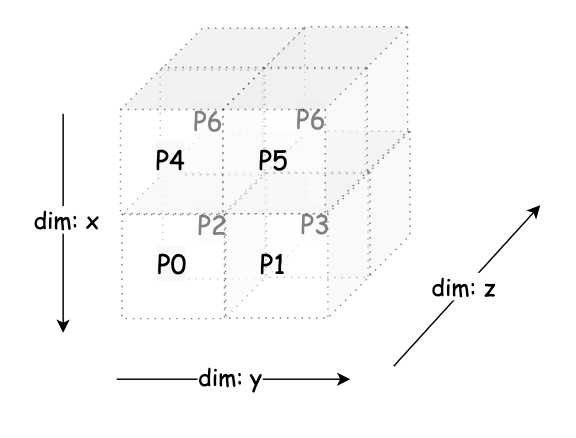
进一步的我们可以想一想,利用 8 个 GPU 如何实现 3D 并行,即在 3 个维度上进行并行化操作:
dim: x(数据并行):
- 第 1 组数据并行:
[P0, P1, P2, P3] - 第 2 组数据并行:
[P4, P5, P6, P7]
dim: y(流水线阶段):
- 第一列(流水线阶段 1):
[P0, P1, P4, P5] - 第二列(流水线阶段 2):
[P2, P3, P6, P7]
dim: z(张量并行):
- 第 1 组张量并行:
[P0, P2, P4, P6] - 第 2 组张量并行:
[P1, P3, P5, P7]
2.2 dimsMapping/Placements:张量的分布描述
在分布式训练中,描述张量如何在设备网格(Mesh)上分布需要三个关键信息:
- 张量维度(Tensor Dimension, axis):张量的逻辑形状
- 设备网格维度(Device Mesh Dimension, dim):设备集群的逻辑拓扑
- axis 到 dim 的映射关系:张量的每个维度(axis)如何映射到设备网格的维度(dim)
两种常见的描述方式:
- dimsMapping:直接将张量维度与设备网格维度的映射关系用整数列表表示
- placements:通过具体的分片类型(如 Sharded 或 Replicated)来描述每个张量维度的切分方式
示例:
假设张量 的形状为 (即 )。设备网格为 。
我们希望:
- 张量的第 0 维(batch, )映射到 Mesh 的第 1 维
- 张量的第 1 维(seq, )映射到 Mesh 的第 0 维
- 张量的第 2 维(hidden, )不切分,完整保存在每个设备上
用 dimsMapping 表述就是 [1, 0, -1]
- 第 0 维 分布到 Mesh 的第 1 维
- 第 1 维 分布到 Mesh 的第 0 维
- 第 2 维 未切分,完整保存在设备上
placements 的表述就是 ["Sharded", "Sharded", "Replicated"]
- 和 被切分到设备
- 未切分,完整存储
三种常见的分片类型
在 placements 中,常见的分片类型有三种:
- Sharded:张量被切分到多个设备上,每个设备存储张量的一部分
- Replicated:张量完整复制到每个设备上
- Partial:指每个计算设备只拥有部分值,需要通过指定的规约操作才能恢复成全量数据
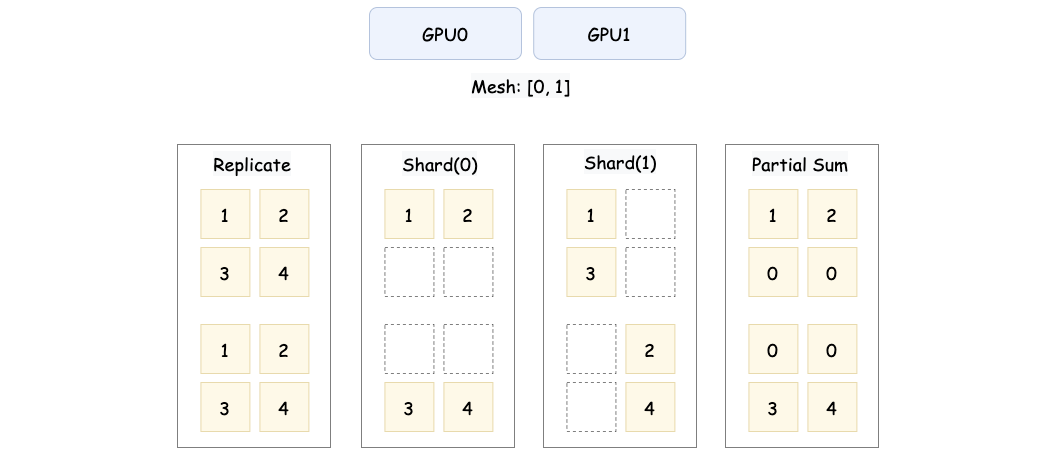
这张图展示了张量在分布式设备上的三种常见分布方式。第一种是 Replicated,即张量的完整数据被复制到每个设备上,所有设备存储的内容完全一致。比如 ,在 GPU0 和 GPU1 上都保存完整的矩阵。
第二种是 Sharded,表示张量被切分到不同设备上,每个设备只存储张量的一部分。按行切分(Sharded(0))时,GPU0 存储 ,GPU1 存储 。按列切分(Sharded(1))时,GPU0 存储 ,GPU1 存储 。
第三种是 Partial,设备存储的不是完整的切片,而是部分计算结果。例如图中的 Partial Sum,GPU0 存储的是原始张量的第 0 行数据 ,GPU1 存储的是原始张量的第 1 行数据 。通过进一步的规约操作(如 AllReduce),可以将所有设备上的部分结果合并为完整张量 。
但是这里有一个问题,dimsMapping 如果是纯数字,那么就没办法表述 Partial 状态,因此如果我们希望某个维度是 Partial 的,那么就 dimsMapping 需要扩展 partial 的状态。我们可以看下 Paddle 里面的例子:
(%463) = "pd_op.cast" (%460) {dtype:float32,op_dist_attr:{mesh:{shape:[2,2],process_ids:[2,3,6,7]},operand(0):{mesh_shape:[2,2],process_ids:[2,3,6,7],dims_mappings:[-1,1], partial(0,SUM), placements:[Partial(reduce_type=SUM), Shard(dim=1)]},result(0):{mesh_shape:[2,2],process_ids:[2,3,6,7],dims_mappings:[-1,1], partial(0,SUM), placements:[Partial(reduce_type=SUM), Shard(dim=1)]},chunk_id:-1},op_role:1,stop_gradient:[false]} : (pd_dist.tensor<4096x4096xf16, mesh_shape:[2,2],process_ids:[2,3,6,7],dims_mappings:[-1,1], partial(0,SUM), placements:[Partial(reduce_type=SUM), Shard(dim=1)]>) -> pd_dist.tensor<4096x4096xf32, mesh_shape:[2,2],process_ids:[2,3,6,7],dims_mappings:[-1,1], partial(0,SUM), placements:[Partial(reduce_type=SUM), Shard(dim=1)]>
我们可以看到这里的 dims_mappings 里面有 partial 的状态,dims_mappings:[-1,1], partial(0,SUM) 表示第 0 纬度是 partial 的,reduce 的方式是 SUM,这样就可以表述 partial 的状态了。
note
其实我感觉这里同时存 Placements 和 dimsMappings 有点冗余,因为 placements 里面已经包含了 dimsMappings 的信息,这里两者都存了,感觉有点冗余。