备战秋招篇-DP 专题
1. 01 背包问题
对于面试的话,其实掌握 01 背包和完全背包,就够用了,最多可以再来一个多重背包。
1.1 朴素动态规划
有 N 件物品和一个容量为 V 的背包。第 i 件物品的体积是 v[i],价值是 w[i]。求解将哪些物品装入背包可使价值总和最大。
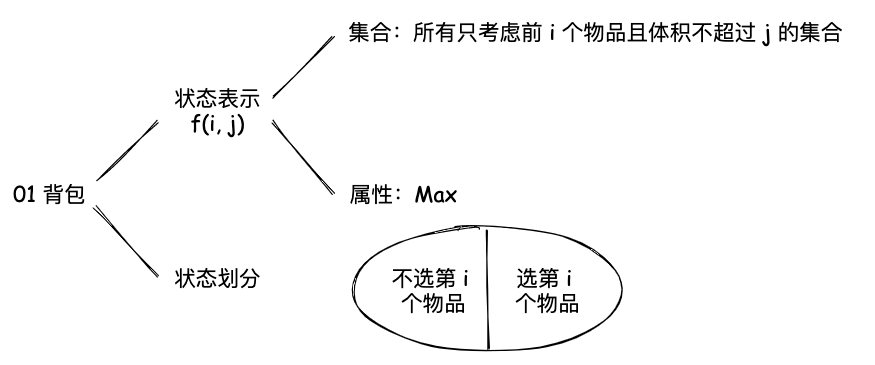
01 背包问题的状态表示是 f(i, j),表示前 i 个物品,背包容量为 j 时的最大价值。它的属性是 Max, 也就是求最大值。对于 f(i, j),可以将其分为两种情况,这样的分法是不重不漏的:
- 第 i 个物品不放入背包,那么
f(i, j) = f(i - 1, j) - 第 i 个物品放入背包,那么
f(i, j) = f(i - 1, j - v[i]) + w[i]
所以,状态转移方程是:
这里给一个简单的模板代码:
int dp[N + 1][V + 1];
int v[N + 1], w[N + 1];
// 省略输入部分
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= N; i++) {
for (int j = 0; j <= V; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= v[i]) {
dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
1.2 优化空间复杂度
在朴素动态规划的基础上,可以发现,f(i, j) 只和 f(i - 1, j) 和 f(i - 1, j - v[i]) 有关,也是说在 i 这个纬度上,只和 i - 1 有关,所以我们可以使用滚动数组的方式,将二维数组优化为一维数组。
但是这里需要注意一个问题,就是如果还是按照朴素版本的遍历方法,那么会出现 f(j) 会被 f(j - v[i]) 更新,但是 j 是大于 j - v[i] 的,计算 j 的时候,j - v[i] 已经被更新过了,也就是说已经不是上一轮的值了,所以这里需要从大到小遍历。
接下来我们看看代码怎么写:
int dp[V + 1]; // 一维数组
int v[N + 1], w[N + 1];
// 省略输入部分
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= N; i++) {
for (int j = V; j >= v[i]; j--) {
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
}
}
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
这题是 01 背包问题的变种,我们可以将这个问题转化为背包问题,背包的容量为 sum / 2,每个物品的体积和价值都是 nums[i],最后看看是否能够刚刚好装满背包。
这个问题的状态表示是 f(i, j),表示前 i 个物品,背包容量为 j 时,是否可以刚刚好装满背包。它的属性是 True/False,也就是求是否存在解。
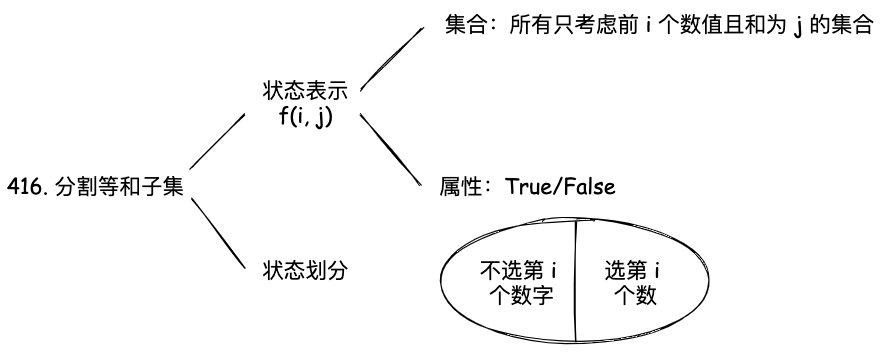
状态转移方程是:
表示的是第 i 个物品放入背包,第 i 个物品如果可以恰好放入背包,那么 也应该是 True。
代码如下:
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
int n = nums.size();
for (auto a: nums) sum += a;
if (sum % 2) return false;
vector<int> dp(sum / 2 + 1);
dp[0] = 1;
for (int i = 0;i < n;i ++)
{
for (int j = sum / 2;j >= nums[i];j --)
{
dp[j] = max(dp[j], dp[j - nums[i]]);
}
}
return dp[sum / 2] > 0;
}
};
注意由于这里的状态表示是是否能够刚刚好装满背包,所以我们需要考虑下初始化的问题,当背包容量为 0 的时候,是可以刚刚好装满的,所以 dp(0) = 1 。
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果 x == y,那么两块石头都会被完全粉碎;
- 如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块石头。返回此石头最小的可能重量 。如果没有石头剩下,就返回 0。
这题如果没见过真的很难想到是动态规划,所以动规还是要多写多见(Doge)
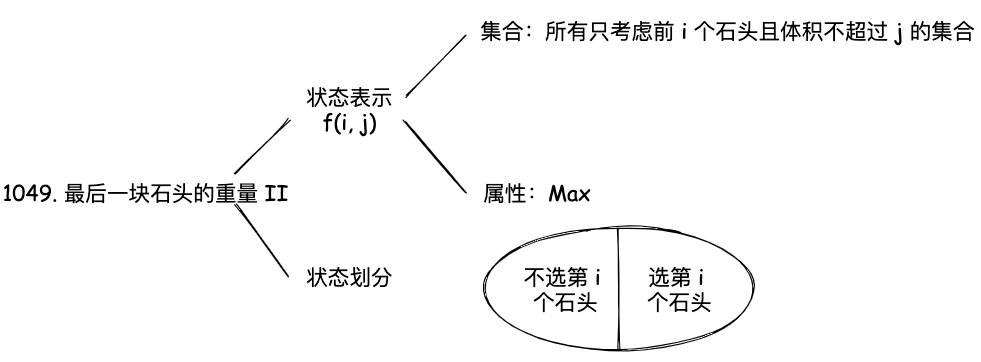
首先我们先看看他的状态表示是什么,这里我们可以用一个背包问题来表示,我们可以将这个问题转化为背包问题,背包的容量为 sum / 2,每个物品的体积和价值都是 stones[i],最后看看最多能装多少。可以看到转化后就是一个标注的 01 背包问题。
tip
为什么是看最多能装多少,而不是刚刚好装满呢?因为这里是求最后一块石头的最小重量,所以我们需要尽可能的装满背包,所以这里是求最多能装多少,装的最多也就是消掉最多。
在最后我们还需要思考一下答案是什么,dp[sum / 2] 表示最多能装多少,也可以理解为把石头分为两堆,使得其中一堆的重量尽可能接近总重量的一半。另一堆的重量就是总重量减去这一堆的重量,也就是 sum - dp[sum / 2]。用较大的减去较小的,就是最后一块石头的最小重量。最终答案就是 sum - 2 * dp[sum / 2]。
下面我们来看看代码:
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int n = stones.size();
int sum = 0;
for (auto a: stones) sum += a;
int target = sum / 2;
vector<int> dp(target + 1);
for (int i = 0;i < n;i ++)
{
for (int j = target;j >= stones[i];j --)
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
return sum - dp[target] - dp[target];
}
};
2915. 和为目标值的最长子序列的长度
给你一个下标从 0 开始的整数数组 nums 和一个整数 target 。
返回和为 target 的 nums 子序列中,子序列 长度的最大值 。如果不存在和为 target 的子序列,返回 -1 。
子序列 指的是从原数组中删除一些或者不删除任何元素后,剩余元素保持原来的顺序构成的数组。
这题和上面的题目416. 分割等和子集很像,但是这里是求最长的子序列,所以我们需要记录的是长度,而不是是否存在解。
状态表示是 f(i, j),表示前 i 个物品,和为 j 时的最长子序列长度。它的属性是 Max,也就是求最大值。不过这里的最大值是长度,而不是价值。注意 01 背包接这类恰好装满的问题,我们需要考虑初始化的问题,当背包容量为 0 的时候,是可以刚刚好装满的,序列长度为 0,所以 dp[0] = 0。而且这里还需要考虑 j-nums[i] 是否在数组内,如果不在数组内,那么 dp[j] = INT_MIN, 为什么要是 INT_MIN 呢?因为这里是求最大值,如果不在数组内,那么就是不合法的,所以应该是负无穷。如果设置的比较小,因为每次 dp[j] = max(dp[j], dp[j - nums[i]] + 1),万一被加到大于 0,那么就会出现错误。
note
这类恰好装满的问题,经常需要考虑初始化的问题,但并不是说其他的 01 背包问题就不需要初始化,比如朴素的 01 背包问题,我们也需要初始化,只不过初始化的值是 0。
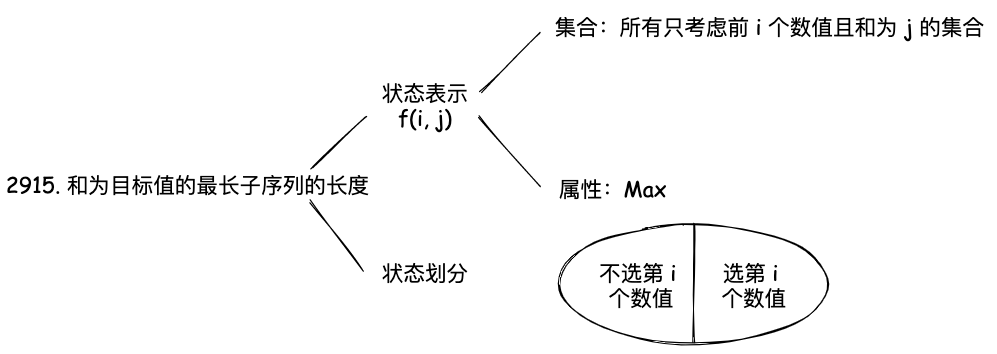
状态转移方程是:
代码如下:
class Solution {
public:
int lengthOfLongestSubsequence(vector<int>& nums, int target) {
int n = nums.size();
vector<int> dp(target + 1, INT_MIN);
dp[0] = 0;
for (int i = 0;i < n;i ++)
{
for (int j = target;j >= nums[i];j --)
dp[j] = max(dp[j], dp[j - nums[i]] + 1);
}
return dp[target] > 0 ? dp[target] : -1;
}
};
494. 目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
这题在普通求目标和的基础上,给每个数添加了正负号,并且需要记录方案数,我们可以看到这里的本质还是求和为 target 的方案数。
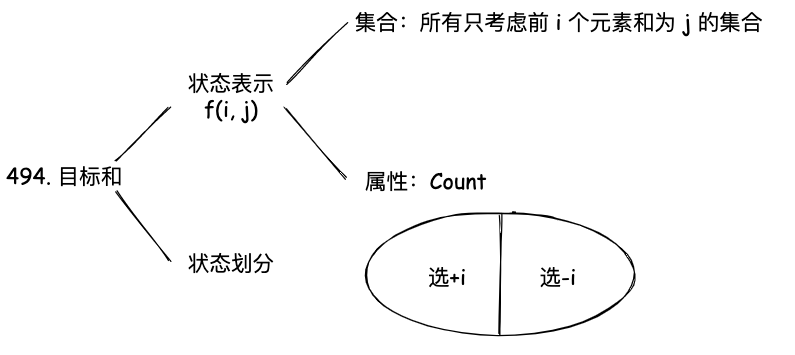
状态表示是 f(i, j),表示前 i 个物品,和为 j 时的方案数。它的属性是 Sum,也就是求和。在状态划分的时候,对于 f(i, j),可以将其分为两种情况,也就是 i 取 +nums[i] 和 -nums[i]。因为这题里面是每个元素都要取的,这点和普通的 01 背包问题不一样。所以 f(i, j) 就可以由 f(i - 1, j - nums[i]) 和 f(i - 1, j + nums[i]) 转移过来。最终可以得到状态转移方程是:
这里需要注意由于 i 状态依赖于 i - 1 的状态, 但是是需要用到 j - nums[i] 和 j + nums[i] 的状态,所以这里我们就没办法使用滚动数组的方式来优化空间复杂度了,因为无论是从小到大还是从大到小,都会出现 j - nums[i] 和 j + nums[i] 的状态被更新的问题。
代码如下:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int n = nums.size();
int sum = 0;
for (int i: nums) sum += i;
if (abs(target) > sum) return 0;
int offset = sum;
vector<vector<int>> dp(n + 1, vector<int>(2 * sum + 1));
dp[0][offset] = 1;
for (int i = 1;i <= n;i ++)
{
for (int j = -sum;j <= sum;j ++)
{
if (j - nums[i - 1] >= -sum)
dp[i][j + offset] += dp[i - 1][j - nums[i - 1] + offset];
if (j + nums[i - 1] <= sum)
dp[i][j + offset] += dp[i - 1][j + nums[i - 1] + offset];
}
}
return dp[n][target + offset];
}
};
这个题目里面还有一个小技巧,因为 target 的值可能是负数,所以我们需要有一个偏移量 offset,这样就可以将负数转化为正数,这样就可以使用数组来表示了。
474. 一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
这题也是 01 背包 的一个变种,这题里面物品的体积有俩个维度,一个是 0 的个数,一个是 1 的个数,然后求的是最大的子集长度。
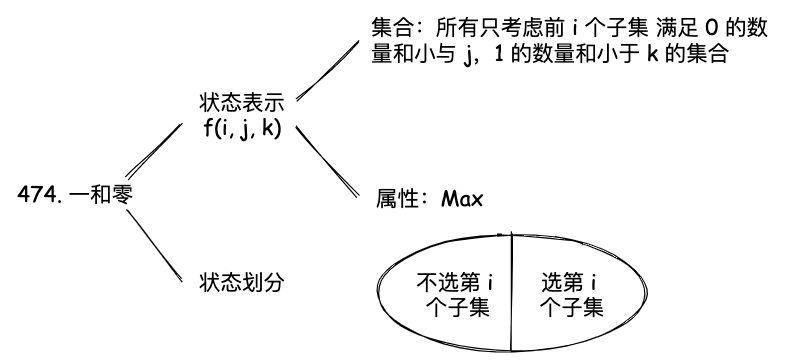
状态表示是 f(i, j, k),表示前 i 个物品,0 的个数为 j,1 的个数为 k 时的最大子集长度。它的属性是 Max,这里的最大值是长度,而不是价值,对应的我们的状态表示里面对应的也是长度。状态转移方程是:
代码如下:
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int len = strs.size();
vector<int> zero_count(len, 0);
vector<int> one_count(len, 0);
for (int i = 0;i < len;i ++)
{
auto s = strs[i];
for (char c: s)
{
if (c == '0') zero_count[i] ++;
else if (c == '1') one_count[i] ++;
}
}
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for (int i = 1;i <= len;i ++)
{
int one_num = one_count[i - 1];
int zero_num = zero_count[i - 1];
for (int j = m;j >= zero_num;j --)
{
for (int k = n;k >= one_num;k --)
{
dp[j][k] = max(dp[j][k], dp[j - zero_num][k - one_num] + 1);
}
}
}
return dp[m][n];
}
};
小结
通过这几道题目可以发现,01 背包的问题的变种基本都是 判断是否可以刚刚好装满 的问题。
比如,416. 分割等和子集 其实就是求是否存在元素和刚刚好是 sum/2, 1049. 最后一块石头的重量 II 也是如出一辙。在 是否刚刚好能装满的问题 上还可以进一步变种,比如记录方案数 (2915. 和为目标值的最长子序列的长度)。在记录状态数的基础上,还可以进一步变种,比如 494. 目标和,这里在记录方案数的基础上,还需要记录正负号。
万变不离其宗,遇到这类问题的解题目思路还是一样的,首先判断是不是 01 背包的问题,然后去想状态表示,然后再去想状态转移方程。最后再去考虑初始化的问题。
2. 完全背包问题
完全背包问题和 01 背包问题的区别在于,每个物品可以取无限次。
完全背包的状态表示和 01 背包一样,也是 f(i, j),表示前 i 个物品,背包容量为 j 时的最大价值。它的属性是 Max,也就是求最大值。对于 f(i, j),可以将其分为两种情况:
- 第 i 个物品不放入背包,那么
f(i, j) = f(i - 1, j) - 第 i 个物品放入背包,那么
f(i, j) = f(i, j - v[i]) + w[i]
为什么第 i 个物品放入背包的时候,是 f(i, j - v[i]) 而不是 f(i - 1, j - v[i]) 呢?因为这里是完全背包问题,每个物品可以取无限次,所以还是取第 i 个物品,只是容量变为了 j - v[i]。
这里由于 f(i, j - v[i]) 不在依赖于 i - 1,所以我们在把它优化成一维数组的时候,可以从小到大遍历。
模板代码如下:
int dp[V + 1]; // 一维数组
int v[N + 1], w[N + 1];
// 省略输入部分
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= N; i++) {
for (int j = v[i]; j <= V; j++) {
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
}
}
518. 零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
这题就是一个板子题,完全背包问题,每个硬币可以取无限次。但是这里的测试用力比较坑,虽然保证了有解的时候结果符合 32 位带符号整数,但是当没有解的时候,结果可能会超过 32 位带符号整数,所以我们需要做俩次动态规划,第一次是求是否有解,第二次是求解的个数。
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int> dp(amount + 1), valid(amount + 1);
dp[0] = 1;
valid[0] = 1;
for (int coin: coins)
{
for (int i = coin;i <= amount;i ++)
valid[i] |= valid[i - coin];
}
if(!valid[amount]) return 0;
for (int coin: coins)
{
for (int i = coin;i <= amount;i ++)
dp[i] += dp[i - coin];
}
return dp[amount];
}
};
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
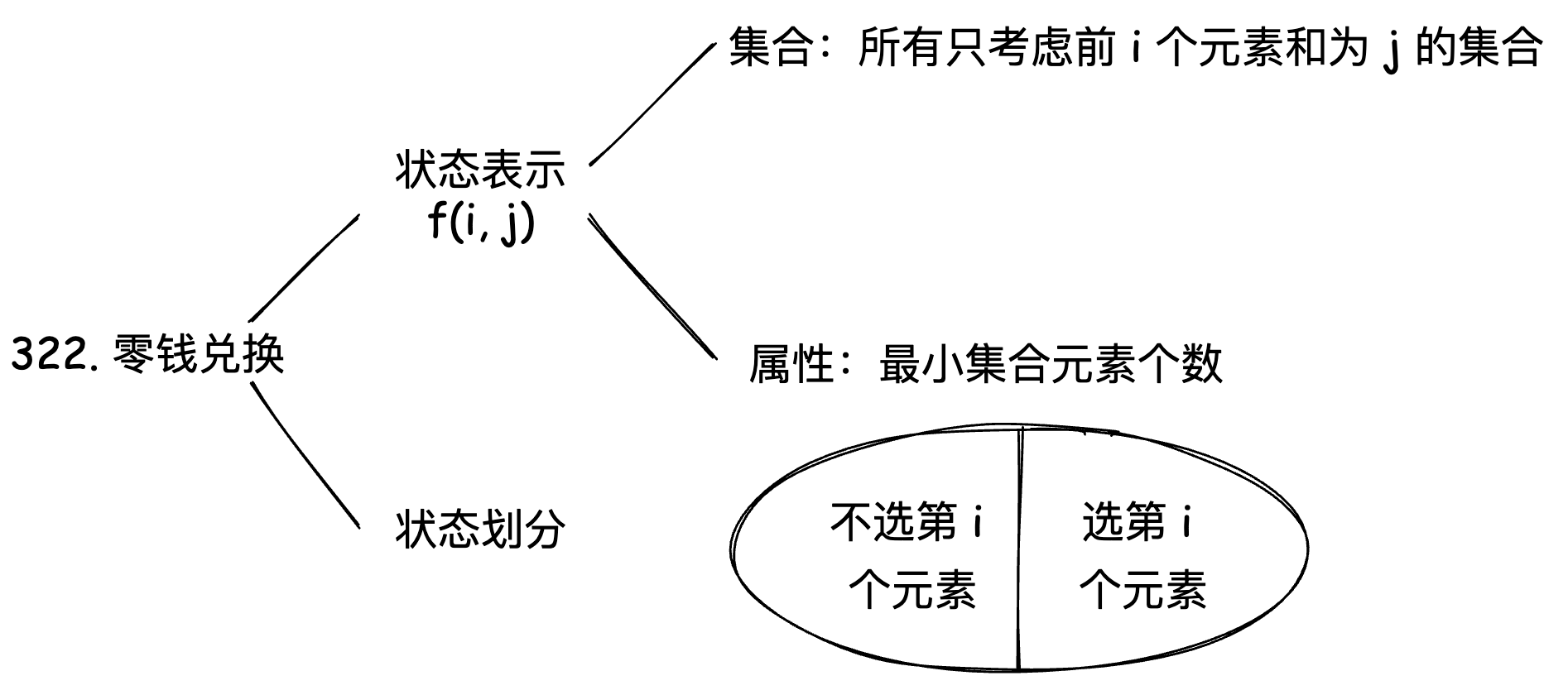
这题我们需要求的是和为 j 且硬币个数最少的方案数,所以我们需要初始化为 INT_MAX,这样在状态转移的时候,可以取最小值。状态表示 f(i, j) 还是表示前 i 个物品,和为 j 时的最少硬币个数。它的属性最小集合的大小,所以状态转移方程是:
代码如下:
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
vector<int> dp(amount + 1, INT_MAX - 1);
dp[0] = 0;
for (int coin: coins)
{
for(int i = coin;i <= amount;i ++)
dp[i] = min(dp[i - coin] + 1, dp[i]);
}
return dp[amount] < INT_MAX - 1 ? dp[amount] : -1;
}
};
279. 完全平方数
给你一个整数 n ,返回和为 n 的完全平方数的最少数量。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
这题的思路和 322. 零钱兑换 是一样的,只不过这里的硬币是完全平方数。我们可以先把完全平方数都找出来,然后再用完全背包的思路来做,比较简单这里就直接放代码了。
class Solution {
public:
int numSquares(int n) {
vector<int> nums;
int i = 0;
while (i * i <= n)
{
nums.push_back(i * i);
i ++;
}
int m = nums.size();
vector<int> dp(n + 1, INT_MAX - 1);
dp[0] = 0;
for (int i = 0;i < m;i ++)
{
for (int j = nums[i]; j <= n;j ++)
dp[j] = min(dp[j], dp[j - nums[i]] + 1);
}
return dp[n];
}
};
小结
完全背包和 01 背包的区别在于,每个物品可以取无限次。题目的类型相比较 01 背包问题要少一些,思路相对来说比较简单一些。最常见的一类题目就是组合数的问题,比如 518. 零钱兑换 II,322. 零钱兑换,279. 完全平方数 等他们本质上都是求组合数。
3. 多重背包问题
多重背包问题和 01 背包问题的区别在于,每个物品可以取多次。多重背包问题可以转换为 0/1 背包问题,我们只需要将每个物品的多次选择视为多个不同的物品,然后使用标准的 0/1 背包算法来解决就可以了。
假设有 3 个物品,分别为:
- 物品 1:重量 2,价值 3,可以放入背包最多 3 次。
- 物品 2:重量 3,价值 4,可以放入背包最多 2 次。
- 物品 3:重量 4,价值 5,可以放入背包最多 1 次。
并且有一个背包,容量为 8。我们可以将物品 1 拆分成 3 个物品,物品 2 拆分成 2 个物品,物品 3 拆分成 1 个物品,这样就可以转化为 0/1 背包问题。
- 物品 1 拆解为 3 个物品:(重量 2,价值 3)、(重量 2,价值 3)、(重量 2,价值 3)
- 物品 2 拆解为 2 个物品:(重量 3,价值 4)、(重量 3,价值 4)
- 物品 3 拆解为 1 个物品:(重量 4,价值 5)
这样就可以转化为 0/1 背包问题,然后使用标准的 0/1 背包算法来解决。
纯的多重背包,Leetcode 上没有,但是有用多重背包来解排列的问题,这个题目我们在下一个小结中再介绍。
4. 看起来像背包问题的排列问题
有一类题目,看起来像背包问题,但是实际上是排列问题。这类题目的特点是,每个物品可以取多次,但是取的顺序是有关系的,比如排列问题。
为什么背包不能解决排列问题呢?因为背包问题是求组合数,不能区分顺序,而排列问题是求排列数,需要区分顺序。
377. 组合总和 Ⅳ
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
这题一看起来你可能以为是一个完全背包问题,但是实陵上是一个排列问题。这里的状态表示是 f(i),表示所有划分方案的集合。它的属性是集合中的元素数量。对于 f(i) 我们可以将其以 nums[j] 为结尾的所有方案的集合的和,状态转移方程是:
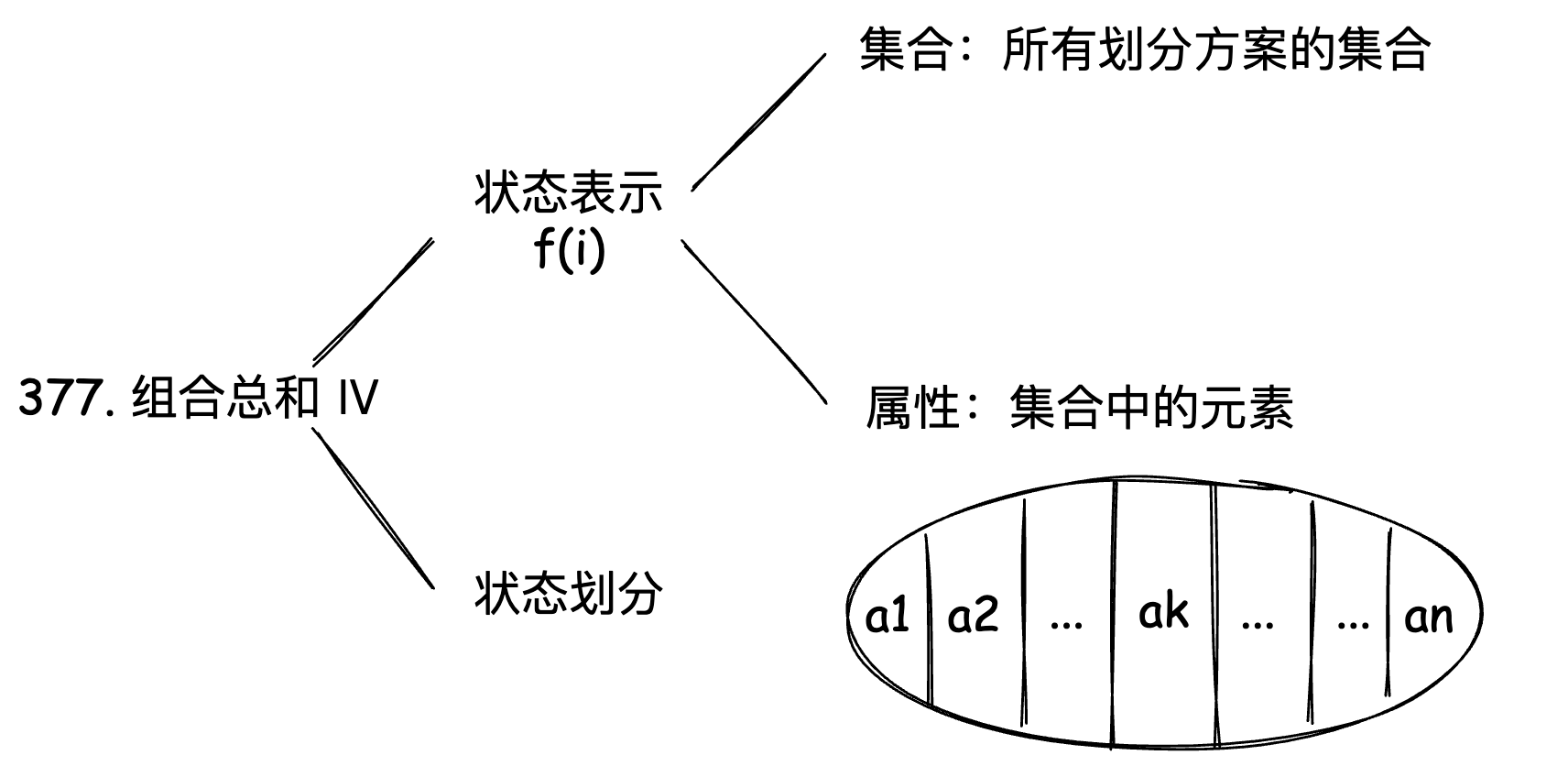
代码如下:
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
vector<unsigned> dp(target + 1);
dp[0] = 1;
for (int j = 0;j <= target;j ++)
for (int num: nums)
{
if (j - num >= 0)
dp[j] += dp[j - num];
}
return dp[target];
}
};
5. 经典线性 DP
5.1 什么是线性 DP
线性 DP 是一种动态规划方法,其中每个状态的值仅依赖于前一个状态的值,而不依赖于更前面的状态。这种方法通过递推关系逐步计算出最终结果,通常用于解决具有线性结构的问题,如最长递增子序列、斐波那契数列等。
下面我们来看看一些经典的线性 DP 问题。
5.2 最长公共子序列(LCS)
一般来说,求两个字符串的最长公共子序列,我们可以使用动态规划来解决。这个问题的状态表示是 f(i, j),表示 text1[0, i] 和 text2[0, j] 的最长公共子序列的长度。它的属性是 Max,也就是求最大值。对于 f(i, j),我们可以将其分为两种情况:
text1[i] == text2[j],那么f(i, j) = f(i - 1, j - 1) + 1text1[i] != text2[j],那么f(i, j) = max(f(i - 1, j), f(i, j - 1))
这个问题的状态转移方程是:
这里看起来和背包问题一样由于每次状态只依赖于前一个状态,但是这里并不能使用滚动数组来优化空间复杂度,因为我们需要用到 f(i - 1, j - 1) 和 f(i, j - 1) 的状态,所以我们还是需要使用二维数组来存储状态。
1143. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
这题就是最长子序列的模板题,下面是代码:
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int n = text1.size();
int m = text2.size();
text1 = " " + text1;
text2 = " " + text2;
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
for (int i = 1;i <= n;i ++)
{
for (int j = 1;j <= m;j ++)
{
if (text1[i] == text2[j])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[n][m];
}
};
583. 两个字符串的删除操作
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
这题和上面的题目基本是一样的,但是我们需要多考虑一些情况,这题里面有可能 word1 和 word2 是一样的情况,这个时候我们就不需要删除了,直接返回 0,如果 word1 和 word2 每个字符都不一样,那么我们就需要删除所有的字符,所以返回 n + m。要怎么才能兼顾考虑这俩种情况呢?我们可以先求出最长公共子序列的长度,然后用 n + m - 2 * lcs 就可以了。
为什么是 n + m - 2 * lcs 呢?因为我们需要删除的字符数是 n - lcs 和 m - lcs,所以总共需要删除的字符数是 n + m - 2 * lcs。
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size();
int m = word2.size();
word1 = " " + word1;
word2 = " " + word2;
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
for (int i = 1; i <= n; i ++)
{
for (int j = 1; j <= m;j ++)
{
if (word1[i] == word2[j])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i - 1][j], dp[i][ j - 1]);
}
}
return n + m - 2 * dp[n][m];
}
};
类似的题目还有 712. 两个字符串的最小 ASCII 删除和,这题和上面的题目基本一样,只不过我们需要求的是删除字符的 ASCII 码的和。
72. 编辑距离
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
这题比较经典,我们可以使用动态规划来解决。这个问题的状态表示是 f(i, j),表示 word1[0, i] 和 word2[0, j] 的最小操作数。它的属性是 Min,也就是求最小值。对于 f(i, j),我们可以将其分为俩种情况:
word1[i] == word2[j],那么f(i, j) = f(i - 1, j - 1)word1[i] != word2[j],那么f(i, j) = min(f(i - 1, j), f(i, j - 1), f(i - 1, j - 1)) + 1f(i - 1, j)表示删除word1[i]f(i, j - 1)表示插入word2[j]f(i - 1, j - 1)表示替换word1[i]为word2[j]
为什么这个问题可以分解到只考虑“最后一位字符”的操作?
想象一下,A[1..i] 要变成 B[1..j],最终达成匹配的那一刻有且只有两种情况:
- A[i] 与 B[j] 已经是相同的字符,此时不需要对 A[i] 或 B[j] 再进行任何修改,那么最终的编辑次数就等于将 A[1..i-1] 变成 B[1..j-1] 的编辑次数 f[i-1][j-1]
- A[i] 与 B[j] 不同或者不匹配,需要通过一次“操作”来让最终的状态达成一致
重点是,任何一个将 A[1..i] 变为 B[1..j] 的最优编辑方案的“最后一步”一定涉及到 A[i] 和/或 B[j]。为什么?因为当你完成了整个转换,A 和 B 最终对齐匹配,其中最后一个字符位置的关系,是最直观、最底层的分界。
让我们从最后一步入手,把所有的可能性细分:
- 情况 1:增加操作 假设最后一步是“在 A 的末尾增加一个字符”,以使得 A[1..i] 变成了 B[1..j]。如果最后一步是增加,那么增加的一定是 B[j],因为你最终想匹配到 B 的末尾。这时,在增加 B[j] 之前,你的 A[1..i] 应该已经与 B[1..j-1]匹配了。所以此时的编辑距离是:f[i][j] = f[i][j-1] + 1(先把 A[1..i] 变成 B[1..j-1],然后再增加一个字符 B[j],总步数 = 前面步骤数 + 1)
- 情况 2:删除操作 假设最后一步是从 A 中删除掉它的最后一个字符 A[i],这样才能与 B[1..j]匹配。 如果要删除 A[i],那么在删除之前 A[1..i-1] 一定已经与 B[1..j] 匹配了。 所以 f[i][j] = f[i-1][j] + 1。
- 情况 3:替换操作 假设最后一步是对 A[i] 进行替换,使它变成 B[j]。 那么在替换前,A[1..i-1] 与 B[1..j-1] 已经匹配完成。然后再将 A[i] 改成 B[j], 所以 f[i][j] = f[i-1][j-1] + 1。(如果 A[i] != B[j])
- 情况 4:什么都不做 如果最后一个字符已经匹配(A[i] == B[j]),那么根本不需要对最后一位进行增删改操作。 此时 f[i][j] = f[i-1][j-1]。(+0 操作,因为已经匹配好了)
通过这四种情况,我们将“最后一步操作”这个问题进行完整划分。增、删、改、或无需操作,这四种情况不重不漏地覆盖了所有可能的编辑方式。
关键点在于, 无论你的最优解原本是在哪个位置动手操作的,因为操作的独立性和可交换性(不影响最终编辑距离),你总能将最后一步安排在 A[i] 和 B[j] 的位置。这样,我们就可以放心地只考虑对 A[i]、B[j] 末尾字符的操作。
每次处理最后那个待匹配字符”的流程。就像搭积木一样:要让前 i 个积木搭成与另一堆前 j 块一样的造型,你不是最后再去动中间的积木,因为如果中间没对齐,你早就应该前面阶段就把它对齐了。从整体到局部,再从局部到最后一块,所有中间步骤加上合理的重排,都可以抽象为在解决 f[i][j] 时,对最后一块拼上、拆下或者改一下。
前面都分析清楚了之后,我们就可以写出状态转移方程了:
此外我们还需要考虑初始化的问题,当 i = 0 或者 j = 0 的时候,我们需要初始化 f(i, j) 的值,这个时候 f(i, j) 的值就是 i 或者 j。因为当 i = 0 的时候,word1[0, 0] 为空字符串,所以我们需要删除 j 个字符,所以 f(0, j) = j。同理,当 j = 0 的时候,f(i, 0) = i。
代码如下:
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size();
int m = word2.size();
word1 = " " + word1;
word2 = " " + word2;
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
for (int i = 0;i <= n;i ++)
dp[i][0] = i;
for (int i = 0;i <= m;i ++)
dp[0][i] = i;
for (int i = 1;i <= n;i ++)
{
for (int j = 1;j <= m;j ++)
{
if (word1[i] == word2[j])
dp[i][j] = dp[i - 1][j - 1];
else
dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
}
}
return dp[n][m];
}
};
97. 交错字符串
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错组成的。
交错字符串的定义如下:s3 是由 s1 和 s2 交错组成的当且仅当可以通过 s1 和 s2 的所有字符按顺序构成 s3,且对于所有的字符,s1 和 s2 中每种字符的出现次数都保持不变。
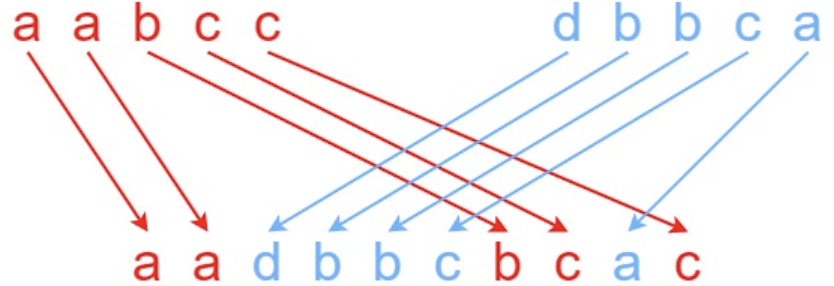
我们首先来看看这个问题的状态表示,这个问题的状态表示是 f(i, j),表示 s1[0, i] 和 s2[0, j] 是否可以交错组成 s3[0, i + j]。它的属性是 True/False。对于 f(i, j),我们可以将其分为俩种情况:
- s3[i + j] == s1[i],那么
f(i, j) = f(i - 1, j) - s3[i + j] == s2[j],那么
f(i, j) = f(i, j - 1)
代码实现如下:
class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int n = s1.size(), m = s2.size(), k = s3.size();
if (n + m != k) return false;
s1 = " " + s1, s2 = " " + s2, s3 = " " + s3;
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
dp[0][0] = 1;
for (int i = 0;i <= n;i ++)
{
for (int j = 0; j <= m;j ++)
{
if (i && dp[i - 1][j] && s1[i] == s3[i + j])
dp[i][j] = 1;
else if (j && dp[i][j - 1] && s2[j] == s3[i + j])
dp[i][j] = 1;
}
}
return dp[n][m];
}
};
注意这里 s1 或者 s2 是可能为空字符串的,所以我们需要初始化 dp[0][0] = 1,而且遍历的时候,我们需要考虑 i 或者 j 为 0 的情况。
1035. 不相交的线
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,我们可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]- 且线不重叠
请注意,满足上述要求的直线可能不存在。
返回两个列表中可以绘制的最长不相交直线的数量。
这题其实就是求最长公共子序列,代码一点都没有变,这里就不放代码了。
1092. 最短公共超序列
给出两个字符串 str1 和 str2,返回同时以 str1 和 str2 作为子序列的最短字符串。如果答案不唯一,则可以返回满足条件的任意一个答案。
如果从字符串 t 中删除一些字符(也可能不删除),可以得到字符串 s,那么 s 就是 t 的一个子序列。
其实这一类问题最重要的就是要把他转换成一个最长公共子序列的问题,这样就可以直接套用上面的模板了。我们来看看这题用最长公共子序列的思路要如何解决。
首先我们需要求出 str1 和 str2 的最长公共子序列的长度,然后根据 DP 数组的信息,我们可以反推出俩个字符串的最长公共子序列。然后我们就可以发现,只要把 str1 和 str2 非公共的字符插入到最长公共子序列中,就可以得到一个最短的公共超序列。
代码如下:
class Solution {
public:
string shortestCommonSupersequence(string str1, string str2) {
int n = str1.size(), m = str2.size();
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
// Step 1: Compute the LCS using DP
for (int i = 1;i <= n;i ++)
{
for (int j = 1;j <= m;j ++)
{
if (str1[i- 1] == str2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// Step 2: Backtrack to find the LCS
string lcs;
int i = n, j = m;
while (i > 0 && j > 0)
{
if (str1[i - 1] == str2[j - 1])
{
lcs.push_back(str1[i - 1]);
i --, j --;
} else if (dp[i - 1][j] > dp[i][j - 1])
{
i --;
} else
{
j --;
}
}
reverse(lcs.begin(), lcs.end());
// Step 3: Construct the shortest common supersequence
i = j = 0;
string res = "";
for (char c: lcs)
{
while (i < str1.size() && str1[i] != c)
res.push_back(str1[i ++]);
while (j < str2.size() && str2[j] != c)
res.push_back(str2[j ++]);
res.push_back(c);
i ++, j ++;
}
for (;i < str1.size();i ++) res.push_back(str1[i]);
for (;j < str2.size();j ++) res.push_back(str2[j]);
return res;
}
};
小结
LCS 的核心是:在两个序列中找到最大匹配的子序列,且必须保持相对顺序。
一旦你发现题目满足以下特点,大概率可以直接套用 LCS 模板:
- 双序列:题目提供两个序列(字符串、数组等),并让你在两者间找“公共”或“相似”的部分。
- 相对顺序:子序列的顺序不能被打乱,但不要求连续。
- 最大化或最小化:通常是找最长的公共部分,或者计算最少的修改/操作次数。
- 允许调整:比如通过插入、删除、替换等方式,让两序列“对齐”。
tip
双序列,顺序在,求长短,可动态
当题目让你在两个序列中找“共同部分”、优化某种代价时,试着问自己:
- “双序列,顺序不乱”:两个序列是否需要相对顺序?
- “动态有解”:问题是否能拆分成子问题,用 DP 解决?
5.3 最长递增子序列(LIS)
最长递增子序列(Longest Increasing Subsequence,简写 LIS)是一个非常经典的问题。所谓最长递增子序列是指,在一个序列中,找到一个最长的子序列,使得这个子序列是严格递增的。
300. 最长递增子序列
这题就是最长递增子序列的模板题,我们可以使用动态规划来解决。这个问题的状态表示是 f(i),表示 nums[0, i] 的最长递增子序列的长度。它的属性是 Max,也就是求最大值。对于 f(i),我们可以将其分为 i 种情况,也就是 nums[i] 可以作为最长递增子序列的最后一个元素,那么 f(i) 就是 f(j) + 1,其中 j 是所有小于 i 的元素中,nums[j] < nums[i] 的最大值。
下面我们来看看代码:
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n + 1);
for (int i = 1;i <= n;i ++)
{
for (int j = 1;j <= i;j ++)
{
if (nums[i - 1] > nums[j - 1])
dp[i] = max(dp[i], dp[j]);
}
dp[i] += 1;
}
int ans = 0;
for (int i = 1;i <= n;i ++)
ans = max(ans, dp[i]);
return ans;
}
};
注意这里的答案是 dp[i] 中的最大值,而不是 dp[n],因为 dp[i] 表示的是 nums[0, i] 的最长递增子序列的长度,所以我们需要遍历一遍 dp 数组,找到最大值。
2826. 将三个组排序
给你一个整数数组 nums 。nums 的每个元素是 1,2 或 3。在每次操作中,你可以删除 nums 中的一个元素。返回使 nums 成为 非递减 顺序所需操作数的 最小值。
这题其实就是最长递增子序列的变种题,但是这里我们需要注意一下,如果要让 nums 成为非递减顺序,那么我的动态规划条件就是 nums[i] >= nums[j],而不是 nums[i] > nums[j]。这里我们需要注意一下。最后的 daan 就是 n - LIS。
class Solution {
public:
int minimumOperations(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n + 1);
int ans = 0;
for (int i = 1;i <= n;i ++)
{
for (int j = 1;j <= n;j ++)
{
if (nums[i - 1] >= nums[j - 1])
dp[i] = max(dp[i], dp[j]);
}
dp[i] += 1;
ans = max(ans, dp[i]);
}
return n - ans;
}
};
1671. 得到山形数组的最少删除次数
我们定义 arr 是 山形数组 当且仅当它满足:
arr.length >= 3- 存在某个下标
i(从0开始) 满足0 < i < arr.length - 1且:arr[0] < arr[1] < ... < arr[i - 1] < arr[i]arr[i] > arr[i + 1] > ... > arr[arr.length - 1]
给你整数数组 nums ,请你返回将 nums 变成 山形状数组 的最少删除次数。
这题如果不会最长递增子序列,那真是写不了一点,首先我们先看下什么是山形数组,山形数组就是一个数组,它的前半部分是递增的,后半部分是递减的。那么我们可以在俩个方向上分别求出最长递增子序列,然后遍历每个位置 i,把俩个方向的最长递增子序列相加,然后用 n 减去这个值就是答案在这个位置的最小删除次数。最后我们遍历一遍所有的位置,找到最小的删除次数。
class Solution {
public:
int minimumMountainRemovals(vector<int>& nums) {
int n = nums.size();
vector<int> f1(n + 1);
vector<int> f2(n + 1);
for (int i = 1;i <= n;i ++)
{
for (int j = 1;j <= i;j ++)
{
if (nums[i - 1] > nums[j - 1])
f1[i] = max(f1[i], f1[j]);
}
f1[i] += 1;
}
for (int i = n; i >= 1;i --)
{
for (int j = n;j >= i;j --)
{
if (nums[i - 1] > nums[j - 1])
f2[i] = max(f2[i], f2[j]);
}
f2[i] += 1;
}
int ans = INT_MAX;
for (int i = 2;i < n;i ++)
{
if (f1[i] > 1 && f2[i] > 1)
ans = min(ans, n - f1[i] - f2[i] + 1);
}
return ans;
}
};
1626. 无矛盾的最佳球队
假设你是球队的经理。对于即将到来的比赛,你想组合一支总体得分最高的球队。球队的得分是球队中所有球员的分数 总和 。
然而,球队中的矛盾会限制球员的发挥,所以必须选出一支 没有矛盾 的球队。如果一名年龄较小球员的分数 严格大于 一名年龄较大的球员,则存在矛盾。同龄球员之间不会发生矛盾。
给你两个列表 scores 和 ages,其中每组 scores[i] 和 ages[i] 表示第 i 名球员的分数和年龄。请你返回 所有可能的无矛盾球队中得分最高那支的分数 。
这题的类型是排序 + 动态规划。我们对球员按照分数进行排序,如果分数相同就按照年龄进行排序。
比如 scores = [4,5,6,5], ages = [2,1,2,1] 排序之后就是:
(4, 2), (5, 1), (5, 1), (6, 2)
答案就是 5 + 5 + 6 = 16。可以观察到这个问题就被转化为了一个最长递增子序列的问题。我们求一个最长递增子序列,使得年龄是递增的,然后把这个最长递增子序列的分数相加就是答案。
class Solution {
public:
int bestTeamScore(vector<int>& scores, vector<int>& ages) {
int n = scores.size();
vector<pair<int, int>> a(n);
for (int i = 0;i < n;i ++)
a[i] = {scores[i], ages[i]};
sort(a.begin(), a.begin() + n);
vector<int> dp(n + 1);
for (int i = 0;i < n;i ++)
{
for (int j = 0;j < i;j ++)
{
if (a[j].second <= a[i].second)
dp[i] = max(dp[i], dp[j]);
}
dp[i] += a[i].first;
}
return *max_element(dp.begin(), dp.begin() + n);
}
};
小结
LIS 的核心是:在一个序列中找到最长的子序列,使得这个子序列是严格递增的。
一旦你发现题目满足 “给你一条序列”,并要求在这条序列上找一个满足某种单调性(一般是递增/非递减/递减/非递增)的子序列 “最长/最短/最多/最少” 时,大概率可以直接套用 LIS 模板。
LCS vs. LIS:
- 如果有两条序列、或者题意就是“公共子序列”之类关键词,就往 LCS 思路走
- 如果题干只有一条序列且在说“递增 / 递减 / 保留子序列单调性”,就往 LIS 思路靠
6. 状态机 DP
什么是“状态”?
状态是描述系统在某一时刻的具体情况。想象一下,你玩一个游戏,每一时刻你的游戏角色都有不同的情况,比如位置、是否有钥匙、生命值等。这些具体的情况就是状态。
什么是“状态机”?
状态机是一种工具,用于描述系统如何从一个状态转移到另一个状态。它类似于一个地图,展示了不同状态之间的连接和转移规则。
想象你在一个建筑里,每个房间代表一个状态,门代表你从一个房间(状态)到另一个房间(状态)的转移。
例如:
- 房间 A:你在起点。
- 房间 B:你拿到了钥匙。
- 房间 C:你打开了大门。
你可以从 A 通过拿钥匙进入 B,然后从 B 通过打开大门进入 C。
状态机 DP 结合了状态机和 动态规划(DP) 的思想,用于解决那些涉及多个状态和状态转移的复杂问题。它通过定义所有可能的状态及其转移方式,逐步计算出问题的最优解。
一般定义 f[i][j] 表示前缀 a[:i] 在状态 j 下的最优解,一般 j 很小。
为什么需要状态机 DP?
有些问题不仅仅是线性推进的,而是涉及到多个条件或阶段,每个阶段可能有不同的状态和选择。状态机 DP 可以系统地处理这些多状态和多转移的情况。 它不像线性 DP 那样只考虑当前状态和前一个状态,而是考虑了更多的状态和转移。
6.1 买卖股票的最佳时机系列
122. 买卖股票的最佳时机 II
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
这题是一个典型的状态机 DP 问题,我们可以定义 f[i][j] 表示第 i 天的状态是 j 的最大利润。其中 j 有俩种状态,一种是持有股票,一种是不持有股票。对于 f[i][0],我们可以从 f[i - 1][0] 和 f[i - 1][1] + prices[i] 转移过来,对于 f[i][1],我们可以从 f[i - 1][1] 和 f[i - 1][0] - prices[i] 转移过来。

下面我们考虑一下初始化的问题,当 i = 0 的时候,f[0][0] 就是 0,f[0][1] 就是 -prices[0] 或者是 -INF 也行主要目的就是确保不会从 f[0][1] 转移到其他状态。代码如下:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n + 1, vector<int>(2));
dp[0][0] = 0;
dp[0][1] = INT_MIN;
for (int i = 1;i <= n;i ++)
{
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i - 1]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i - 1]);
}
return dp[n][0];
}
};
309. 买卖股票的最佳时机含冷冻期
给定一个整数数组 prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)
这题和上一题的区别就是多了一个冷冻期,我们还是可以定义 f[i][j] 表示前 i 天的状态是 j 的最大利润。 但是对于 f[i][1] 的转移方程就有所不同了,我们可以从 f[i - 1][1] 和 f[i - 2][0] - prices[i] 转移过来。代码如下:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n + 2, vector<int>(2));
dp[1][1] = INT_MIN;
for (int i = 0;i < n;i ++)
{
dp[i + 2][0] = max(dp[i + 1][0], dp[i + 1][1] + prices[i]);
dp[i + 2][1] = max(dp[i + 1][1], dp[i][0] - prices[i]);
}
return dp[n + 1][0];
}
};
188. 买卖股票的最佳时机 IV
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
这题在上一题的基础上加了一个交易次数的限制,我们可以定义 f[i][j][k] 表示前 i 天,最多交易 j 次的状态是 k 的最大利润。其中 k 有俩种状态,一种是持有股票,一种是不持有股票。
对于 f[i][j][0],我们可以从 f[i - 1][j][0] 和 f[i - 1][j][1] + prices[i] 转移过来,对于 f[i][j][1],我们可以从 f[i - 1][j][1] 和 f[i - 1][j - 1][0] - prices[i] 转移过来。这里需要注意 i 是从 0 开始的,表示 prices 的索引,而 j 是从 1 开始的,表示交易次数。为了避免 i - 1 为负数,我们让 i 从 1 开始,相对应的 j 要从 2 开始。
我们还需要考虑一下初始化的问题,当 i = 0 的时候,f[0][k][0] 就是 0,f[0][k][1] 就是 -prices[0] 或者是 -INF 。
代码如下:
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int n = prices.size();
vector<vector<vector<int>>> f(n + 1, vector<vector<int>>(k + 2, vector<int>(2, INT_MIN / 2)));
for (int j = 1;j <= k + 1;j ++)
f[0][j][0] = 0;
for (int i = 0;i < n;i ++)
{
for (int j = 1;j <= k + 1;j ++)
{
f[i + 1][j][0] = max(f[i][j][0], f[i][j][1] + prices[i]);
f[i + 1][j][1] = max(f[i][j][1], f[i][j - 1][0] - prices[i]);
}
}
return f[n][k + 1][0];
}
};
1493. 删掉一个元素以后全为 1 的最长子数组
给你一个二进制数组 nums ,你需要从中删掉一个元素。
请你在删掉元素的前提下,返回最长的全为 1 的子数组的长度。
这题为什么是一个状态机 DP 问题呢?
我们可以定义两个状态:
dp[i][0] 表示以 i 结尾,尚未删除过任何元素,所能得到的连续 1 的最大长度。 dp[i][1] 表示以 i 结尾,已经删除过一个元素(无论删的是 0 还是 1),所能得到的连续 1 的最大长度。
对于 dp[i][0],我们可以从 dp[i - 1][0] 转换过来,如果 nums[i] 是 1 的话,那么 dp[i][0] = dp[i - 1][0] + 1,如果 nums[i] 是 0 的话,就相当于断开了,所以 dp[i][0] = 0。对于 dp[i][1],如果 nums[i] 是 1 的话,那么 dp[i][1] = dp[i - 1][1] + 1,如果 nums[i] 是 0 的话,就相当于删掉了一个 0,所以 dp[i][1] = dp[i - 1][0] + 1。
class Solution {
public:
int longestSubarray(vector<int>& nums) {
int n = nums.size();
bool all_one = true;
for (int i: nums)
if (i != 1)
{
all_one = false;
break;
}
if (all_one) return n - 1;
vector<vector<int>> dp(n + 1, vector<int>(2));
int ans = INT_MIN;
for (int i = 0;i < n;i ++)
{
if (nums[i] == 1)
{
dp[i + 1][0] = dp[i][0] + 1;
dp[i + 1][1] = dp[i][1] + 1;
} else {
dp[i + 1][0] = 0;
dp[i + 1][1] = dp[i][0];
}
ans = max(ans, dp[i + 1][1]);
}
return ans;
}
};
3259. 超级饮料的最大强化能量
来自未来的体育科学家给你两个整数数组 energyDrinkA 和 energyDrinkB 。你可以从中选择一个数组,并从中选择一个整数作为能量增强剂。
你需要每小时饮用一种能量饮料来 最大化 你的总强化能量。然而,如果从一种能量饮料切换到另一种,你需要等待一小时来梳理身体的能量体系(在那个小时里你将不会获得任何强化能量)。
返回在接下来的 n 小时内你能获得的 最大 总强化能量。
注意 你可以选择从饮用任意一种能量饮料开始。
这题其实就是上面 买卖股票的最佳时机冷冻期 的变种题,我们可以定义 f[i][j] 表示前 i 个小时,状态是 j 的最大强化能量。其中 j 有俩种状态,一种是喝了 energyDrinkA,一种是喝了 energyDrinkB。对于 f[i][0],我们可以从 f[i - 1][0] 和 f[i - 1][1] + energyDrinkA[i - 1] 转移过来,对于 f[i][1],我们可以从 f[i - 1][1] 和 f[i - 1][0] + energyDrinkB[i - 1] 转移过来。
代码如下:
class Solution {
public:
long long maxEnergyBoost(vector<int>& energyDrinkA, vector<int>& energyDrinkB) {
int n = energyDrinkA.size();
vector<vector<long long>> dp(n + 2, vector<long long>(2));
for (int i = 0;i < n;i ++)
{
dp[i + 2][0] = max(dp[i + 1][0], dp[i][1]) + energyDrinkA[i];
dp[i + 2][1] = max(dp[i + 1][1], dp[i][0]) + energyDrinkB[i];
}
return max(dp[n + 1][0], dp[n + 1][1]);
}
};
2786. 访问数组中的位置使分数最大
给你一个下标从 0 开始的整数数组 nums 和一个正整数 x。
你 一开始 在数组的位置 0 处,你可以按照下述规则访问数组中的其他位置:
- 如果你当前在位置 i ,那么你可以移动到满足 i < j 的 任意 位置 j
- 对于你访问的位置 i ,你可以获得分数 nums[i]
- 如果你从位置 i 移动到位置 j 且 nums[i] 和 nums[j] 的 奇偶性 不同,那么你将失去分数 x
请你返回你能得到的 最大 得分之和
注意 ,你一开始的分数为 nums[0]
我们从左往右遍历数组,遍历到一个元素时,如果选择移动到这个位置,那么移动到这个位置所能获得的最大分数,只取决于之前的位置中:
- 最后移动的元素为偶数时得分的最大值
- 最后移动的元素为奇数时得分的最大值
只要知道这两个值,我们可以选择从偶数值位置移动过来,也可以从奇数值位置移动过来,得分加上当前数组值。当与当前位置的数组值奇偶性不同时,得分需要额外减去 x。两者的最大值就是移动到当前位置可以获得的最大得分。
代码如下:
class Solution {
public:
long long maxScore(vector<int>& nums, int x) {
long long res = nums[0];
vector<long long> dp(2, INT_MIN);
dp[nums[0] % 2] = nums[0];
for (int i = 1; i < nums.size(); i++) {
int parity = nums[i] % 2;
dp[parity] = max(dp[parity] + nums[i], dp[1 - parity] - x + nums[i]);
res = max(res, dp[parity]);
}
return res;
}
};
1262. 可被三整除的最大和
给你一个整数数组 nums,请你找出并返回能被三整除的元素 最大和。
这题其实和上一题非常类似,上一题是在位置 i 可以从前面 的奇偶性不同的地方移动过来,这题是在位置 i 可以从前面余数不同的地方移动过来。
代码如下:
class Solution {
public:
int maxSumDivThree(vector<int>& nums) {
vector<int> dp{0, INT_MIN, INT_MIN};
for (int i = 1;i <= nums.size();i ++)
{
vector<int> f = dp;
for (int j = 0;j < 3;j ++)
{
// dp[j] => dp[(j + nums[i - 1]) % 3]
int b = (nums[i - 1] + j) % 3;
f[b] = max(f[b], dp[j] + nums[i - 1]);
}
dp = move(f);
}
return dp[0];
}
};
为什么我们需要额外使用一个数组 f 呢?因为我们需要保证 dp 的值是上一次的值,而不是本次的值。所以我们需要额外使用一个数组来保存上一次的值。
PS:这题余数真的很绕,我也是看了好久才看懂的。
1911. 最大子序列交替和
一个下标从 0 开始的数组的 交替和 定义为 偶数 下标处元素之 和 减去 奇数 下标处元素之 和 。
- 比方说,数组 [4,2,5,3] 的交替和为 (4 + 5) - (2 + 3) = 4 。
给你一个数组 nums ,请你返回 nums 中任意子序列的 最大交替和 (子序列的下标 重新 从 0 开始编号)。
一个数组的 子序列 是从原数组中删除一些元素后(也可能一个也不删除)剩余元素不改变顺序组成的数组。比方说,[2,7,4] 是 [4,2,3,7,2,1,4] 的一个子序列(加粗元素),但是 [2,4,2] 不是。
定义 f[i][0] 表示前 i 个数中长为偶数的子序列的最大交替和, f[i][1] 表示前 i 个数中长为奇数的子序列的最大交替和。
初始时有 f[0][0]=0,f[0][1]=-INF。
对于第 i 个数,有选或不选两种决策。
状态转移方程为:
- f[i][0] = max(f[i-1][0], f[i-1][1]+nums[i])
- f[i][1] = max(f[i-1][1], f[i-1][0]-nums[i])
用滚动数组优化空间复杂度,代码如下:
class Solution {
public:
long long maxAlternatingSum(vector<int>& nums) {
long long ans = 0;
int n = nums.size();
vector<long long> dp = {0, INT_MIN};
for (int i = 0;i < n;i ++)
{
long long a = dp[0], b = dp[1];
dp[0] = max(a, b - nums[i]);
dp[1] = max(b, a + nums[i]);
}
return dp[1];
}
};
1186. 删除一次得到子数组最大和
给你一个整数数组,返回它的某个 非空 子数组(连续元素)在执行一次可选的删除操作后,所能得到的最大元素总和。换句话说,你可以从原数组中选出一个子数组,并可以决定要不要从中删除一个元素(只能删一次哦),(删除后)子数组中至少应当有一个元素,然后该子数组(剩下)的元素总和是所有子数组之中最大的。
注意,删除一个元素后,子数组 不能为空。
这题也是比较明显的状态机 DP 问题,对于每个位置有 2 种可能,一种是这个位置是从已经删除过一个元素的地方移动过来的,一种是这个位置是从没有删除过元素的地方移动过来的。
对于没有删除过元素的地方,从前一个没有删除过元素的地方移动过来,我们也可以不选前面的元素(前面的最大子数组和是负的)
对于删除过元素的地方,从前一个删除过元素的地方移动过来,也可以从前一个没有删除过元素的地方移动过来(删除当前元素)。
class Solution {
public:
int maximumSum(vector<int>& arr) {
int n = arr.size();
vector<vector<int>> f(n + 1, vector<int>(2, INT_MIN / 2));
int ans = INT_MIN;
for (int i = 0;i < n;i ++)
{
f[i + 1][0] = max(f[i][0], 0) + arr[i];
f[i + 1][1] = max(f[i][1] + arr[i], f[i][0]);
ans = max(f[i + 1][0], ans);
ans = max(f[i + 1][1], ans);
}
return ans;
}
};
小结
状态机 DP 的核心是:在一个序列中找到多个状态之间的最优转移。
一旦你发现题目满足以下特点,大概率可以直接套用状态机 DP 模板:
- 多状态:题目涉及多个状态(如持有股票、不持有股票等)。
- 状态转移:状态之间有明确的转移规则。
- 最优解:需要在多个状态之间找到最优解。
状态机 DP 的关键是定义好状态和状态转移方程,然后通过动态规划的方法逐步计算出最优解。
tip
多状态,转移清,求最优,可动态
当题目让你在多个状态之间找到最优解时,试着问自己:
- “多状态,转移清”:问题是否涉及多个状态和状态转移?
- “动态有解”:问题是否能拆分成子问题,用 DP 解决?
通过这几道题目可以发现,状态机 DP 的问题的变种基本都是 判断多个状态之间的最优转移 的问题。遇到这类问题的解题思路还是一样的,首先判断是不是状态机 DP 的问题,然后去想状态表示,然后再去想状态转移方程。最后再去考虑初始化的问题。
7. 划分型 DP
7.1 判定能否划分
一般定义 f[i] 表示前 i 个数是否可以划分成满足条件的子集。
枚举最后一个子数组的左端点 j,判断从 j 到 i 的子数组是否满足条件。
2369. 检查数组是否存在有效划分
给你一个下标从 0 开始的整数数组 nums ,你必须将数组划分为一个或多个 连续 子数组。
如果获得的这些子数组中每个都能满足下述条件 之一 ,则可以称其为数组的一种 有效 划分:
- 子数组 恰 由 2 个相等元素组成,例如,子数组 [2,2]
- 子数组 恰 由 3 个相等元素组成,例如,子数组 [4,4,4]
- 子数组 恰 由 3 个连续递增元素组成,并且相邻元素之间的差值为 1 。例如,子数组 [3,4,5] ,但是子数组 [1,3,5] 不符合要求
如果数组 至少 存在一种有效划分,返回 true ,否则,返回 false
在判断「可否将序列划分为若干满足条件的子序列」时,往往可以用 DP 来做。我们常见的思路是:令 dp[i] 表示 “从下标 0 到下标 i 这一段子数组,能否被有效地划分?”。如果 dp[i] = true,则意味着前 i+1 个元素可以划分成若干有效子数组;如果 dp[i] = false,则表示不能。
要想知道 dp[i] 的真假,我们需要回过头去看能否从后往前切出一个满足题目要求的子数组(长度可能为 2,也可能为 3),并且切走这段后,前面剩下的那部分也能有效划分。
因此,就会有下面的几种状态转移形式:
- 长度为 2 的子数组:如果 nums[i] == nums[i-1],并且 dp[i-2] = true,那么 dp[i] 可以为 true
- 长度为 3 的子数组:
- 如果 nums[i] == nums[i-1] == nums[i-2] 并且 dp[i-3] = true,那么 dp[i] = true
- 如果 nums[i-2] + 1 == nums[i-1] 且 nums[i-1] + 1 == nums[i] 并且 dp[i-3] = true,那么 dp[i] = true
只要上述任意一种情况成立,则 dp[i] = true
下面我们来看看代码:
class Solution {
public:
bool validPartition(vector<int>& nums) {
int n = nums.size();
vector<int> f(n + 1);
f[0] = 1;
for (int i = 1;i < n;i ++)
{
if (f[i - 1] && nums[i] == nums[i - 1])
f[i + 1] = 1;
else if (i > 1 && f[i - 2] && nums[i] == nums[i - 1]
&& nums[i - 1] == nums[i - 2])
f[i + 1] = 1;
else if (i > 1 && f[i - 2] && nums[i] == nums[i - 1] + 1
&& nums[i - 1] == nums[i - 2] + 1)
f[i + 1] = 1;
}
return f[n];
}
};
139.单词拆分
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
设 表示“从字符串 的起始位置到位置 的这段子字符串(即 )能否被成功拆分”。
如果我们已经定义了 表示到 下标这段子串能否被拆分,那么下一步就是如何通过子问题的结果得到更长子串的可行性。
我们考虑计算 时,需要从字符串前面所有可能的“断点”进行尝试:
假设我们要验证 是否可以拆分成功,就要看它是不是可以由一个更小的可拆分子串 再加上一个在字典中的单词 组合而成。
即:如果 ,并且 ,那么就可以把 拆分成功,让 。
因此,转移方程通常写成:
这里的 “” 表示“逻辑或(OR)”,只要有一个 j 能让前面子串 且 在字典里,就可以让 。
代码如下:
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
int n = s.length();
unordered_set<string> h;
for (auto item: wordDict) h.insert(item);
vector<int> dp(n + 1);
dp[n] = 1;
for (int i = n - 1;i >= 0;i --)
{
string ss = "";
for (int j = i;j < n;j ++)
{
ss += s[j];
// 如果 ss 在哈希表中,且 dp[j + 1] 为 True
// 也就是 s[j + 1, n] 也可以被拆分
// 那么 s[i, n] 也可以被拆分 => dp[i] = 1
if (dp[j + 1] && h.count(ss))
{
dp[i] = 1;
break;
}
}
}
return dp[0];
}
};
7.2 最优划分
计算最少(最多)可以划分出多少段、最优划分得分等。
一般定义 表示长为 的前缀 在题目约束下,分割出的最少(最多)子数组个数(或者定义成分割方案数)。
132. 分割回文串 II
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。
返回符合要求的 最少分割次数 。
示例 1:
输入:s = "aab" 输出:1 解释:只需一次分割就可将 s 分割成 ["aa","b"] 这样两个回文子串。
- 回文判断预处理
对于子串 ,如果我们每次都用双指针去判断是否回文,会导致整体复杂度过高。典型做法:在 的时间内先预处理一个二维数组 isPal[i][j],表示
- 长度为 1 的子串必然回文
- 长度为 2 的子串,当两个字符相等时是回文
- 长度大于 2 的子串,如果首尾字符相等、且去掉首尾后的那段子串也回文,则整段回文
- 动态规划 - 最少切割
定义 dp[i] 表示 “字符串的前 i 个字符(下标从 1 开始计)最少需要切几刀,才能让所有子串均为回文”。
转移方程:枚举最后一段回文串的起点 j,如果 是回文,则
特殊情况:如果整段 本身回文,不需要刀数,即 。
初始化可将 dp[i] 先设成一个较大值,在循环中不断更新最优解,注意 dp[0] 我们初始化为 -1,dp[0] = -1 的好处是,如果后续 j=1,到 i 这一段是回文,就有 dp[0] + 1 = 0,把 dp[i] 赋成 0,表示不需要切割
class Solution {
public:
int minCut(string s) {
int n = s.size();
s = " " + s;
vector<vector<int>> f1(n + 1, vector<int>(n + 1));
vector<int> f2(n + 1, INT_MAX);
for (int i = 0;i <= n;i ++)
{
f1[i][i] = 1;
f1[i][0] = 1;
}
for (int i = 1;i <= n;i ++)
if (s[i] == s[i + 1])
f1[i][i + 1] = 1;
for (int len = 3; len <= n; len ++)
{
for (int i = 1;i <= n - len + 1;i ++)
{
int j = i + len - 1;
if (s[i] == s[j] && f1[i + 1][j - 1])
f1[i][j] = 1;
}
}
f2[0] = -1;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= i; j++)
{
if (f1[j][i])
f2[i] = min(f2[i], f2[j-1] + 1);
}
}
return f2[n];
}
};
813. 最大平均值和的分组
给定数组 nums 和一个整数 k 。我们将给定的数组 nums 分成 最多 k 个非空子数组,且数组内部是连续的 。 分数 由每个子数组内的平均值的总和构成。
注意我们必须使用 nums 数组中的每一个数进行分组,并且分数不一定需要是整数。
返回我们所能得到的最大 分数 是多少。答案误差在 内被视为是正确的。
令 表示将数组的前 个元素分成 个非空子数组的最大分数。
- 表示前 个元素。
- 表示分成 个非空子数组。
- 数组从 开始索引,方便描述(实际代码中可以从 开始)。
我们希望求的是 ,即将整个数组分成 个子数组的最大分数。
要将前 个元素分成 个子数组,可以考虑第 个子数组的结束位置。假设第 个子数组的起始位置是 ,即子数组为 ,那么:
- 前 个元素被分成 个子数组的最大分数为 。
- 第 个子数组的分数为 。
其中,第 个子数组的平均值可以表示为:
因此:
边界条件:
- :0 个元素分成 0 个子数组时的分数为 0。
- 和 是无效状态(可以初始化为负无穷或跳过)。
- 当 时,无法将 个元素分成 个子数组,状态也无效。
在计算 时,可以预处理前缀和数组 :
则:
这样,可以高效计算每段子数组的和,转移方程为:
下面是代码:
class Solution {
public:
double largestSumOfAverages(vector<int>& nums, int k) {
int n = nums.size();
vector<vector<double>> dp(n + 1, vector<double>(k + 1));
vector<double> prefix(n + 1);
for (int i = 1;i <= n;i ++)
prefix[i] = prefix[i - 1] + nums[i - 1];
for (int i = 1; i <= n;i ++)
dp[i][1] = prefix[i] / i;
for (int j = 2;j <= k;j ++)
{
for (int i = 1;i <= n;i ++)
{
for (int p = 1;p < i;p ++)
{
dp[i][j] = max(dp[i][j], dp[p][j - 1] + (prefix[i] - prefix[p]) / (i - p));
}
}
}
return dp[n][k];
}
};
注意这里的遍历顺序,动态规划的核心是:后续状态依赖于前面的状态。因此,计算状态 时,必须确保它所依赖的所有状态已经被计算完毕。
对于这个问题:
- 依赖于 ,其中 。
- 是子问题的结果,表示将前 个元素分成 个子数组的最大分数。
因此,必须在计算 之前,先确保所有可能的 都已计算完成。
遍历顺序为:
- 枚举子数组数量 从 2 到 :
- 因为 个子数组的状态依赖于 个子数组的状态,必须先完成较小子数组数量的计算。
- 枚举元素数量 从 1 到 :
- 因为状态 表示前 个元素的分数,必须确保依赖的前 个元素的状态已被计算。
- 枚举分割点 从 1 到 :
- 枚举第 个子数组的起点 ,计算 。
这种遍历顺序的具体逻辑是:
- 外层 :先分 1 个子数组,再分 2 个子数组……逐渐增加子数组的数量。
- 中层 :对于每个子数组数量 ,逐步考虑数组前缀长度 的分数。
- 内层 :对于前 个元素分成 个子数组,考虑每个可能的分割点 来更新状态。
为什么不能调整顺序?
- 如果先枚举 再枚举 :
- 例如,先计算 和 ,但 依赖于 ,而 本身可能还未完成计算。会导致错误结果。
- 如果不按顺序枚举 :
- 假设直接使用 或某种跳跃的 值,会遗漏可能的子数组分割方案,导致结果不正确。
1278. 分割回文串 III
我们可以用两个状态来解决这个问题:
辅助状态:一个数组 ,表示将字符串 修改为回文串所需的最少修改次数。
这个状态是预处理的,具体计算方法后面会提到。主状态:令 表示将字符串的前 个字符分割成 个回文子串所需的最少修改次数。
如果字符串前 个字符被分成 个回文子串,那么可以考虑最后一个回文子串的起始位置 :
- 假设最后一个回文子串是 ,前 个字符分成 个回文子串。
- 此时状态转移为:
- 其中 表示前 个字符分成 个回文子串的最小修改次数, 表示将 修改为回文串所需的最少修改次数。
边界条件:
- ,即将前 个字符直接修改为一个回文串。
- 当 ,因为无法分成更多的子串。
如果 ,则首尾字符无需修改,只需递归计算中间部分:
如果 ,需要修改其中一个字符:
对所有 ,使用动态规划方式填表。
以下是 C++ 的代码实现:
class Solution {
public:
int palindromePartition(string s, int k) {
int n = s.size();
// 预处理 cost 数组
vector<vector<int>> cost(n, vector<int>(n, 0));
for (int len = 2; len <= n; ++len) { // 子串长度
for (int i = 0; i <= n - len; ++i) {
int j = i + len - 1;
cost[i][j] = cost[i + 1][j - 1] + (s[i] != s[j]);
}
}
// 动态规划数组
vector<vector<int>> dp(n + 1, vector<int>(k + 1, INT_MAX));
// 边界条件:分成 1 个回文子串的情况
for (int i = 1; i <= n; ++i) {
dp[i][1] = cost[0][i - 1];
}
// 状态转移
for (int p = 2; p <= k; ++p) { // 分成 p 个回文子串
for (int i = 1; i <= n; ++i) { // 前 i 个字符
for (int j = 1; j < i; ++j) { // 最后一个子串的起始位置
dp[i][p] = min(dp[i][p], dp[j][p - 1] + cost[j][i - 1]);
}
}
}
return dp[n][k];
}
};
1335. 工作计划的最低难度
定义 表示将前 项任务分配到 天内所能获得的最小总难度。
- 表示前 天。
- 表示前 项任务。
为了完成第 项任务并分配到第 天,可以从第 项任务开始到第 项任务分配给第 天,其中 。
此时,第 天的工作难度是第 到第 项任务中的最大难度。
这里:
- 表示前 项任务分配到前 天的最小总难度。
- 表示从第 项到第 项任务的最大工作难度。
边界条件:
- 无法分配的情况:
- 如果任务数 小于天数 ,则无法分配:。
- 基础情况:
- :即将前 项任务都分配到第 1 天。
为了高效计算 ,可以从右往左遍历 ,逐步更新当天任务的最大难度,避免重复计算。
以下是 C++ 的代码实现:
class Solution {
public:
int minDifficulty(vector<int>& jobDifficulty, int d) {
int n = jobDifficulty.size();
if (n < d) return -1; // 如果任务数小于天数,无法分配
// 动态规划数组
vector<vector<int>> dp(d + 1, vector<int>(n + 1, INT_MAX));
// 边界条件:第一天的最大工作难度
dp[1][0] = 0;
for (int j = 1; j <= n; ++j) {
dp[1][j] = max(dp[1][j - 1], jobDifficulty[j - 1]);
}
// 状态转移
for (int i = 2; i <= d; ++i) { // 枚举天数
for (int j = i; j <= n; ++j) { // 枚举任务数量(至少完成 i 项任务)
int maxDifficulty = 0;
for (int k = j; k >= i; --k) { // 枚举第 i 天的起点
maxDifficulty = max(maxDifficulty, jobDifficulty[k - 1]);
dp[i][j] = min(dp[i][j], dp[i - 1][k - 1] + maxDifficulty);
}
}
}
return dp[d][n];
}
};