Rope For Vit 论文阅读
1. 试图解决的问题
这篇论文旨在解决旋转位置嵌入(RoPE)在视觉变压器(Vision Transformer,ViT)中的应用问题。 RoPE 在语言模型中表现出色,尤其是在变压器的长度外推方面,但其在计算机视觉领域的影响尚未充分探索。本文通过对 RoPE 在 2D 视觉数据中的实际应用进行全面分析,揭示了 RoPE 在增加推理时图像分辨率的同时保持精度的出色外推性能。最终,这种方法在 ImageNet-1k、COCO 检测和 ADE-20k 分割任务中带来了性能提升。研究提供了将 RoPE 应用于 ViT 的详细指南,在最小的额外计算开销下提高骨干网络性能。
2. 相关研究
- 位置嵌入:研究了绝对位置嵌入(APE)和相对位置偏差(RPB)在视觉变压器中的应用。APE通常用于传统的ViT架构,而RPB更适合层次化的ViT,如Swin Transformer 。
- RoPE在视觉建模中的应用:最早的研究将RoPE应用于ViT相关架构,例如Hybrid X-former,它将一维RoPE应用于Vision X-formers。此外,EVA-02引入了二维轴向RoPE,用于新的语言对齐视觉模型 。
- 多分辨率推理:研究了多分辨率推理方法,以改进ViT在下游任务中的性能。CAPE通过连续增强位置嵌入来改善ViT的多分辨率性能。ResFormer通过基于深度卷积的相对位置嵌入实现了多分辨率推理,并提出了一种改进的ViT架构 。
- 条件位置编码:CPE发现卷积网络可以有效地将相对位置信息注入到令牌中,使用3×3深度卷积作为条件位置嵌入 。
- 其他相关工作:包括使用连续增强位置嵌入(CAPE)、通过多分辨率自蒸馏学习改进的ResFormer,以及具有灵活补丁大小的FlexiViT,这些方法在不同的上下文中展示了多分辨率推理的效果 。
3. 如何解决问题
3.1 扩展RoPE到2D输入
研究首先将RoPE从一维扩展到二维,以适应图像数据的特点。采用轴向频率的方法,将嵌入维度分为两部分,分别应用于x轴和y轴。然而,为了更好地处理对角方向的问题,提出了一种混合可学习频率的方法,使得网络能够学习频率参数,进而更适应ViT的注意力机制。
混合可学习频率的计算实现如下:
# 混合可学习频率计算
def compute_mixed_cis(freqs: torch.Tensor, t_x: torch.Tensor, t_y: torch.Tensor, num_heads: int):
N = t_x.shape[0]
# No float 16 for this range
with torch.cuda.amp.autocast(enabled=False):
freqs_x = (t_x.unsqueeze(-1) @ freqs[0].unsqueeze(-2)).view(N, num_heads, -1).permute(1, 0, 2)
freqs_y = (t_y.unsqueeze(-1) @ freqs[1].unsqueeze(-2)).view(N, num_heads, -1).permute(1, 0, 2)
freqs_cis = torch.polar(torch.ones_like(freqs_x), freqs_x + freqs_y)
return freqs_cis
compute_mixed_cis 函数的主要功能是计算二维频率分量,并将其转换为极坐标形式的复数。在这里,freqs 是一个包含两个频率分量的张量,t_x 和 t_y 是两个张量,分别表示 x 和 y 方向的位置编码。num_heads 表示注意力头的数量。freqs_x 和 freqs_y 分别表示 x 和 y 方向的频率分量,计算公式如下:
其中, 和 分别表示 x 和 y 方向的位置编码, 和 分别表示 x 和 y 方向的频率分量。
在计算混合可学习频率时,首先将 t_x 和 t_y 与 freqs 的两个频率分量进行点积运算,然后将结果转换为复数形式。最后,将 x 和 y 方向的频率分量相加,得到最终的频率分量。这样的计算方式可以更好地处理对角方向的问题,提高模型的性能。
为什么这样的计算方式可以更好地处理对角方向的问题呢?这是因为在二维输入中,对角方向的位置编码是由 x 和 y 方向的位置编码共同决定的。因此,通过将 x 和 y 方向的频率分量相加,可以更好地捕捉到对角方向的位置信息,从而提高模型的性能。
RoPE 原论文中给出的二维 RoPE 的计算方法如下:
# 原 RoPE 计算方法
def compute_axial_cis(dim: int, end_x: int, end_y: int, theta: float = 100.0):
freqs_x = 1.0 / (theta ** (torch.arange(0, dim, 4)[: (dim // 4)].float() / dim))
freqs_y = 1.0 / (theta ** (torch.arange(0, dim, 4)[: (dim // 4)].float() / dim))
t_x, t_y = init_t_xy(end_x, end_y)
freqs_x = torch.outer(t_x, freqs_x)
freqs_y = torch.outer(t_y, freqs_y)
freqs_cis_x = torch.polar(torch.ones_like(freqs_x), freqs_x)
freqs_cis_y = torch.polar(torch.ones_like(freqs_y), freqs_y)
return torch.cat([freqs_cis_x, freqs_cis_y], dim=-1)
针对原 Rope 的计算方法,可以补充说一点: 从一维RoPE推广到二维RoPE,和单纯地把每个方向当作一维RoPE再concat(和传统三角式位置编码的扩展方法一样)是等价的
二维RoPE的解如下:
但是我们看下代码实现,其实是分别计算了 x 和 y 方向的 RoPE,然后 concat 在一起。
3.3 实验验证
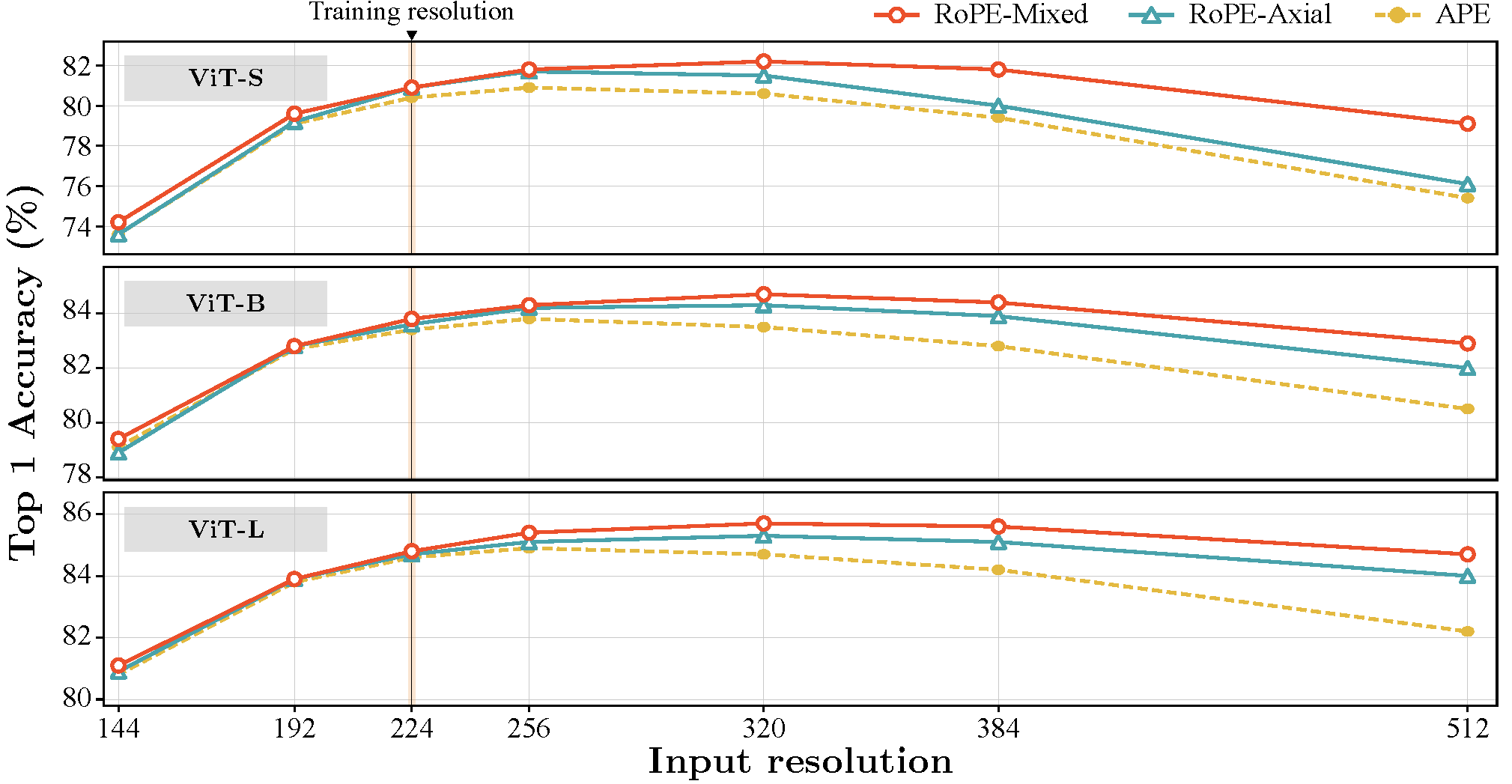
实验部分,研究在ViT和Swin Transformer架构上进行了一系列的测试,验证了2D RoPE的有效性。在ImageNet-1k数据集上进行的多分辨率分类测试显示,2D RoPE在高分辨率图像上的外推性能显著提高。特别是在目标检测和语义分割任务中,使用2D RoPE的ViT和Swin Transformer在MS-COCO和ADE20k数据集上表现出色,显著提升了性能。
DeiT-III
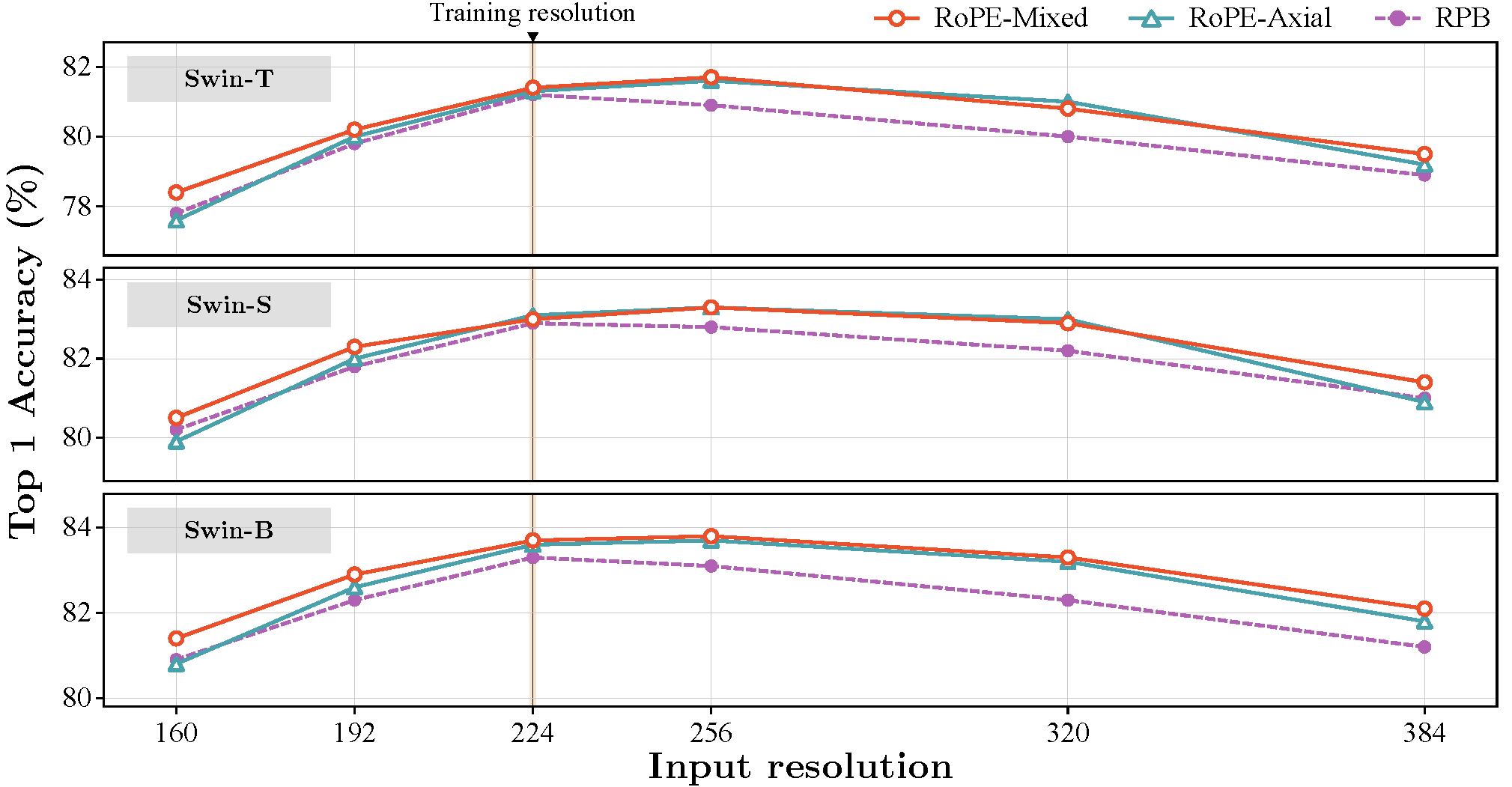
Swin Transformer
4. 总结
这篇论文研究了如何将旋转位置嵌入(RoPE)应用到 Vit 中,从而提升其在图像识别任务中的性能。RoPE在语言模型中已经表现出色,尤其在处理长度外推时。然而,在计算机视觉领域,RoPE的潜力尚未得到充分发掘。
研究首先将RoPE从一维扩展到二维,以适应图像数据的特性。采用了轴向频率和混合可学习频率的方法,使得位置嵌入能够更好地处理不同方向的相对位置。轴向频率将嵌入维度分为两部分,分别应用于x轴和y轴,而混合可学习频率则让网络可以学习和调整频率参数,增强了模型对图像数据的适应性。
在实验中,研究团队对ViT和Swin Transformer进行了详细的测试。结果表明,使用2D RoPE后,这些模型在ImageNet-1k数据集上的多分辨率分类任务中表现显著提升,特别是在高分辨率图像的外推能力上。此外,2D RoPE在目标检测和语义分割任务中也表现优异,在MS-COCO和ADE20k数据集上的性能明显提升。