信息论基础知识

tip

信息论背后的思想: 一件不太可能的事件比一件比较可能的事件更有信息量。

信息 (Information) 需要满足的三个条件:

比较可能发生的事件的信息量要少。
比较不可能发生的事件的信息量要大。
独立发生的事件之间的信息量应该是可以叠加的。例如, 投郑的硬币两次正面朝上传递的信息量, 应该是投郑一次硬币正面朝上的信息量的两倍。

自信息 (Self-Information): 对事件 $x=x$ , 我们定义:

I(x)=-\log P(x)

自信息满足上面三个条件, 单位是奈特 (nats) (底为 $e$ )

香农熵 (Shannon Entropy): 上述的自信息只包含一个事件的信息, 而对于整个概率分布 $P$ , 不确定性可以这样衡量：

\mathbb{E}_{x \sim P}[\mathrm{I}(x)]=-\mathbb{E}_{x \sim P}[\log P(x)]

也可以表示成 $\mathrm{H}(\mathrm{P})$ 。香农熵是编码原理中最优编码长度。

多个随机变量:

联合熵 (Joint Entropy)： 表示同时考虑多个事件的条件下（即考虑联合分布概率）的熵。 $H(X, Y)=-\sum_{x, y} P(x, y) \log (P(x, y))$
条件熵 (Conditional Entropy)： 表示某件事情已经发生的情况下, 另外一件事情的熵。 $H(X \mid Y)=-\sum_{y} P(y) \sum_{x} P(x \mid y) \log (P(x \mid y))$
互信息 (Mutual Information)： 表示两个事件的信息相交的部分。 $I(X, Y)=H(X)+H(Y)-H(X, Y)$
信息变差 (Variation of Information)： 表示两个事件的信息不相交的部分。 $V(X, Y)=H(X, Y)-I(X, Y)$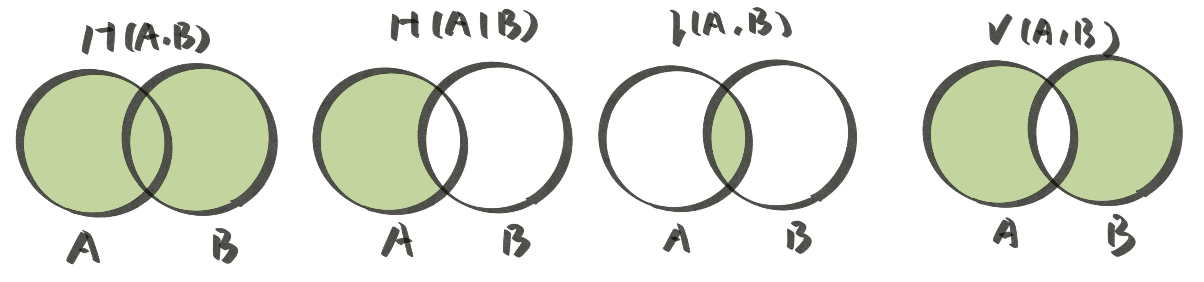

KL 散度 (Kullback-Leibler Divergence) 用于衡量两个分布 $P(\mathrm{x})$ 和 $Q(\mathrm{x})$ 之间的差距:

\mathrm{D}_{\mathrm{KL}}(P \| Q)=\mathbb{E}_{x \sim P}\left[\log \frac{P(x)}{Q(x)}\right]=\mathbb{E}_{x \sim P}[\log P(x)-\log Q(x)]

注意 $\mathrm{D}_{\mathrm{KL}}(\mathrm{P} \| \mathrm{Q}) \neq \mathrm{D}_{\mathrm{KL}}(\mathrm{Q} \| \mathrm{P})$ , 不满足对称性。

交叉熵 (Cross Entropy):

H(P, Q)=H(P)+\mathrm{D}_{\mathrm{KL}}(P \| Q)=-\mathbb{E}_{x \sim P}[\log Q(x)]

假设 $P$ 是真实分布, $Q$ 是模型分布, 那么最小化交叉熵 $\mathrm{H}(\mathrm{P}, \mathrm{Q})$ 可以让模型分布逼近真实分布。

# KL 定义
from scipy.stats import entropy
def kl(p,q):
    """
    D(P || Q)
    """
    p = np.asarray(p, dtype=np.float)
    q = np.asarray(q, dtype=np.float)
    return np.sum(np.where(p != 0,p * np.log(p/q),0))

参考

[1][https://github.com/MingchaoZhu/DeepLearning](https://github.com/MingchaoZhu/DeepLearning)

信息论基础知识

tip

参考​

参考