蒙特卡洛采样

tip

本文大部分内容参考知乎文章，写这篇文章只是方便做注释和总结，参考文献在结尾处

什么是蒙特卡洛

蒙特卡洛原来是一个赌场的名称，用它作为名字大概是因为蒙特卡洛方法是一种随机模拟的方法，这很像赌博场里面的扔骰子的过程。最早的蒙特卡洛方法都是为了求解一些不太好求解的求和或者积分问题。

例如下图是一个经典的用蒙特卡洛求圆周率的问题，用计算机在一个正方形之中随机的生成点，计数有多少点落在1/4圆之中，这些点的数目除以总的点数目即圆的面积，根据圆面积公式即可求得圆周率

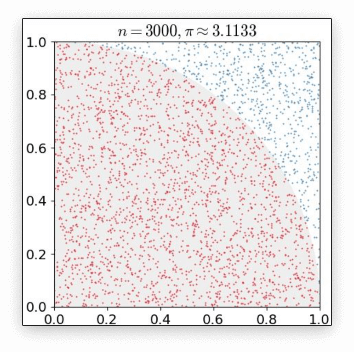
我们可以使用代码模拟一下上述采样的过程：

import random
total = [10, 100, 1000, 10000, 100000, 1000000, 5000000]  #随机点数
for t in total:
    in_count = 0
    for i in range(t):
        x = random.random()
        y = random.random()
        dis = (x**2 + y**2)**0.5
        if dis<=1:
            in_count += 1
    print(t,'个随机点时，π是：', 4*in_count/t)

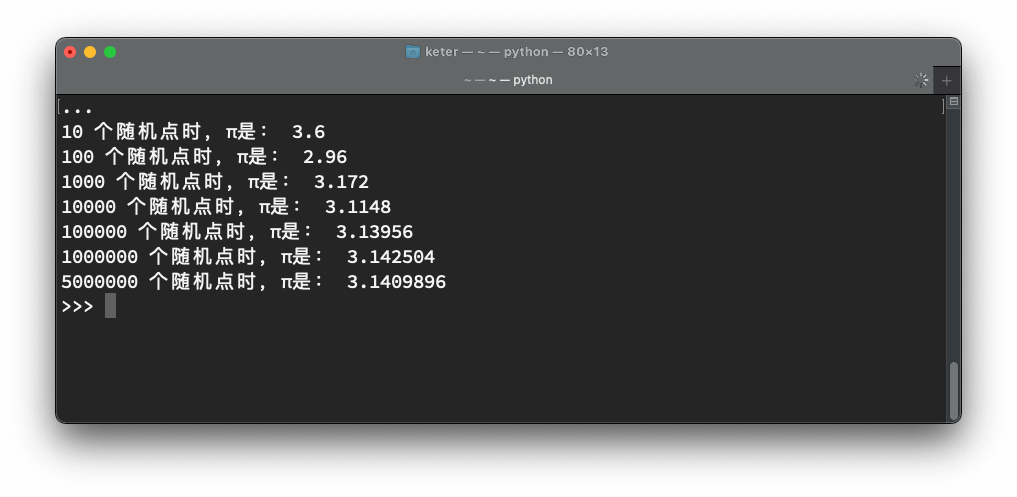可以看出随着随机点数的增加，近似度逐渐增大。

我们可以理解蒙特卡罗算法的一个基本思想，其实就是通过随机点来模拟实际的情况，不断抽样以逼近真实值。

由蒙特卡洛法得出的值并不是一个精确值，而是一个近似值，而且当投点的数量越来越大时，这个近似值也越接近真实值。

蒙特卡洛的应用

通常蒙特卡罗方法可以粗略地分成两类：

一类是所求解的问题本身具有内在的随机性，借助计算机的运算能力可以直接模拟这种随机的过程。例如在核物理研究中，分析中子在反应堆中的传输过程。中子与原子核作用受到量子力学规律的制约，人们只能知道它们相互作用发生的概率，却无法准确获得中子与原子核作用时的位置以及裂变产生的新中子的行进速率和方向。科学家依据其概率进行随机抽样得到裂变位置、速度和方向，这样模拟大量中子的行为后，经过统计就能获得中子传输的范围，作为反应堆设计的依据。

另一种类型是所求解问题可以转化为某种随机分布的特征数，比如随机事件出现的概率，或者随机变量的期望值。通过随机抽样的方法，以随机事件出现的频率估计其概率，或者以抽样的数字特征估算随机变量的数字特征，并将其作为问题的解。这种方法多用于求解复杂的多维积分问题。

蒙特卡洛法求积分

比如积分$\theta=\int_{a}^{b} f(x) d x$， 如果f(x)的原函数很难求解，那么这个积分也会很难求解。

那么我们如何通过蒙特卡罗方法对其进行模拟求解呢？

随机投点法

这个方法和上面的两个例子的方法是相同的。如下图所示，有一个函数f(x)，要求它从a到b的定积分，其实就是求曲线下方的面积：

这时可以用一个比较容易算得面积的矩型罩在函数的积分区间上（假设其面积为Area），然后随机地向这个矩形框里面投点，其中落在函数f(x)下方的点为绿色，其它点为红色，然后统计绿色点的数量占所有点（红色+绿色）数量的比例为r，那么就可以据此估算出函数f(x)从 a 到 b 的定积分为 Area × r。

平均值法（期望法）

如下图所示，在[a,b]之间随机取一点x时，它对应的函数值就是f(x)，我们要计算$\theta=\int_{a}^{b} f(x) d x$，就是图中阴影部分的面积。

一个简单的近似求解方法就是用$f(x)*(b-a)$来粗略估计曲线下方的面积，在[a,b]之间随机取点x，用f(x)代表在[a,b]上所有f(x)的值，如下图所示：

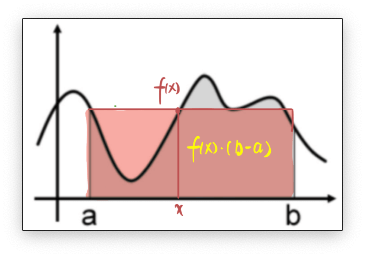
用一个值代表[a,b]区间上所有值太粗糙了，我们可以进一步抽样更多的点，比如下图抽样了四个随机样本$x_1$,$x_2$,$x_3$,$x_4$（满足均匀分布），每个样本都能求出一个近似面积值 $f(x_i)*(b-a)$，然后计算他们的数学期望，就是蒙特卡罗计算积分的平均值法了。

​

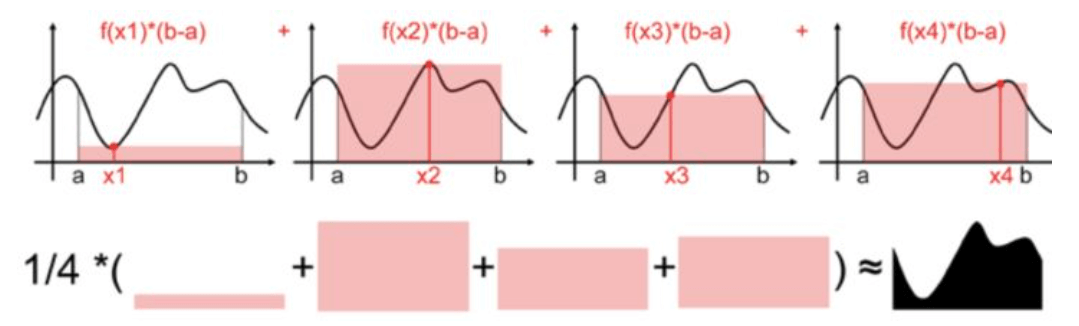
然后进一步我们采样n个随机样本（满足均匀分布)，则有：

$$S=\frac{b-a}{n} \sum_{i=1}^{n} f\left(x_{i}\right) \simeq \theta$$

采样点越多，估计值也就越来越接近。

上面的方法是假定x在[a,b]间是均匀分布的，而大多时候x在[a,b]上不是均匀分布的，因此上面方法就会存在很大的误差。

这时我们假设x在[a,b]上的概率分布函数为$p(x)$, 加入到$\theta=\int_{a}^{b} f(x) d x$中变换为：

$$\theta=\int_{a}^{b} f(x) d x=\int_{a}^{b} \frac{f(x)}{p(x)} p(x) d x \simeq \frac{1}{n} \sum_{i=1}^{n} \frac{f\left(x_{i}\right)}{p\left(x_{i}\right)}$$

这就是蒙特卡罗期望法计算积分的一般形式。

那么问题就换成了如何从p(x)中进行采样。

---

蒙特卡罗采样方法

常见的概率分布采样

如果x在[a,b]的概率分布是我们常见的分布，就可以将其概率分布公式p(x)直接代入:

$$\theta= \frac{1}{n} \sum_{i=1}^{n} \frac{f\left(x_{i}\right)}{p\left(x_{i}\right)}$$

然后进行求解；

例如 在[a,b]之间是均匀分布，此时$p\left(x_{i}\right)=\frac{1}{b-a}$ ，代入上式为 (与上面推导出来的相同):

$$\theta=\frac{1}{n} \sum_{i=1}^{n} \frac{f\left(x_{i}\right)}{1 /(b-a)}=\frac{b-a}{n} \sum_{i=1}^{n} f\left(x_{i}\right)$$

其他常见的分布比如正态分布、t分布，F分布，Beta分布，Gamma分布等，都可以通过标准均匀分布$U(0,1)$来变换生成（标准正态分布是十分容易采样样本的）。在python的numpy，scikit-learn等类库中，都有生成这些常用分布样本的函数可以使用。

不过很多时候，我们的概率分布p(x)不是常见的分布，它的形式可能非常复杂，或者p(x)是个高维的分布，样本的生成可能就很困难了。

接受拒绝采样

当待采样函数P(x)的形式十分复杂时，可以找一个简单的建议分布g(x)，并将其乘一个常数C使其全部在p(x)的上方，如下图所示，红线是我们要采样的p(x)，蓝色曲线为C*g(x):

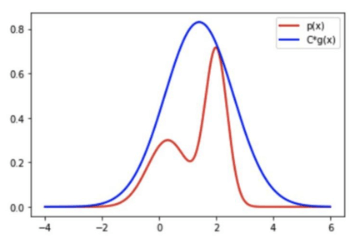
然后思路其实和前面的投点法差不多，就是从均匀分布中随机采样一个点，如果这个点在红色曲线下方，就接受它，如果在红色曲线和蓝色曲线中间，就拒绝这个点。当C*g(x)越接近q(x)时接受率越高，采样效率越高，因此有时他们差距比较大时，就会出现大部分的点都被拒绝，这样效率会非常低。

参考

[1][【智源学院】30分钟了解蒙特卡罗方法-有意思专题系列(蒙特卡洛方法)( Monte Carlo method)哔哩哔哩(-)つロ千杯~- bilibino](https://link.zhihu.com/?target=https%3A//www.bilibili.com/video/BV1Gs411g7EJ%3Fp%3D1%26share_medium%3Dandroid%26share_plat%3Dandroid%26share_source%3DQQ%26share_tag%3Ds_i%26timestamp%3D1619936020%26unique_k%3DsA4JiH) [2]小白都能看懂的蒙特卡洛方法以及 python实现 bitcarmanlee的博客-CSDN博客蒙特卡洛 [3] 蒙特卡洛方法的理解、推导和应用氢键H-H-CSDN博客_蒙特卡洛积分推导](https://link.zhihu.com/?target=https%3A//blog.csdn.net/bitcarmanlee/article/details/82716641) [4][Eureka:马尔可夫链蒙特卡罗算法(MCMC)]((https://link.zhihu.com/?target=https%3A//blog.csdn.net/qq_32618327/article/details/90452846)) [5][如何理解蒙特卡洛方法的接受拒绝采样?](https://zhuanlan.zhihu.com/p/37121528) [6][蒙特卡罗方法详解](https://zhuanlan.zhihu.com/p/369099011)