概率论基础知识
概率
tip
为什么机器学习要使用概率?
因为机器学习通常必须处理不确定量,有时也可能需要处理随机(非确定的)量。不确定性和随机性可能来自多个方面。
变量与随机变量
随机变量
表示随机现象(在一定条件下,并不总是出现相同结果的现象称为随机现象)中各种结果的实值 函数(一切可能的样本点)。例如某一时间内公共汽车站等车乘客人数,电话交换台在一定时间 内收到的呼叫次数等,都是随机变量的实例。
tip
变量与随机变量有什么区别?
当变量取值为1时,变量就变成了随机变量,当随机变量的取值概率为1,随机变量就变成了变量
随机变量和概率分布的联系
一个随机变量只能表示一个可能的状态。概率分布描述的一簇随机变量每个可能的状态;
随机变量可以分为离散型随机变量和连续性随机变量, 相应的描述其概率分布的函数是:
- 概率质量函数:描述离散型随机变量的概率分布
- 概率密度函数:描述连续性随机变量的概率分布
概率质量函数
概率质量函数 (Probability Mass Function): 对于离散型变量, 我们先定义一个随机变量, 然后用 符号来说明它遵循的分布: , 函 数 是随机变量 的 。
例如, 考虑一个离散型 有 个不同的值, 我们可以假设 是均匀分布的 (也就是将它的每个值视为等可能的), 通过将它的 设为:
对于所有的 都成立。
概率密度函数
当研究的对象是连续型时, 我们可以引入同样的概念。如果一个函数 是概率密度函数 (Probability Density Function):
- 分布满足非负性条件:
- 分布满足归一化条件:
例如在 上的均匀分布:这里 表示在 内为 1 , 否则为 0 。
累积分布函数
累积分布函数 (Cummulative Distribution Function) 表示对小于 的概率的积分:
边缘概率 (Marginal Probability):如果我们知道了一组变量的联合概率分布, 但想要了解其中一个子集的概率分布。这种定义在子集上的概率 分布被称为边缘概率分布。
条件概率 (Conditional Probability):在很多情况下,我们感兴趣的是某个事件, 在给定其他事件发生时出现的概率。这种概率叫做条件概率。 我们将给定 发生的条件概率记为 。这个条件概率可以通过下面的公式计算:
条件概率的链式法则 (Chain Rule of Conditional Probability): 任何多维随机变量的联合概率分布, 都可以分解成只有一个变量的条件概率 相乘的形式:
独立性 (Independence): 两个随机变量 和 , 如果它们的概率分布可以表示成两个因子的乘积形式, 并且一个因子只包含 另一个因子只包含 , 我们就称这两个随机变量是相互独立的:
tip
联合概率和边缘概率有什么区别?
联合概率是指多个条件同时发生的概率,而边缘概率是指某个时间发生的概率。两者可以相互转换, 比如当X和Y相互独立的时候有:
随机变量的量度
期望 (Expectation): 函数 关于概率分布 或 的期望表示为由概率分布产生 , 再计算 作用到 上后 的平均值。对于离散型随机变量, 这可以通过求和得到:
对于连续型随机变量可以通过求积分得到:
另外, 期望是线性的:
方差 (Variance): 衡量的是当我们对 依据它的概率分布进行采样时, 随机变量 的函数值会呈现多大的差异, 描述采样得到的函数值在期望上 下的波动程度:
将方差开平方即为标准差 (Standard Deviation)。
协方差 (Covariance): 用于衡量两组值之间的线性相关程度:
注意, 独立比协方差为0要求更强, 因为独立还排除了非线性的相关。
常用概率分布
伯努利分布
伯努利分布 (Bernoulli Distribution) 是单个二值随机变量的分布, 随机变量只有两种可能。它由一个参数 控制, 给出了随机变量等 于 1 的概率:
表示一次试验的结果要么成功要么失败。
tip
什么时候使用可以使用伯努利分布?
伯努利分布适合对离散型的随机变量进行建模,比如投骰子这样的事件就可以使用伯努利分布来对这个时间建模
范畴分布(分类分布)
范畴分布 (Multinoulli Distribution) 是指在具有 个不同值的单个离散型随机变量上的分布:
例如每次试验的结果就可以记为一个 维的向量, 只有此次试验的结果对应的维度记为 1 , 其他记为 0 。
高斯分布(正态分布)
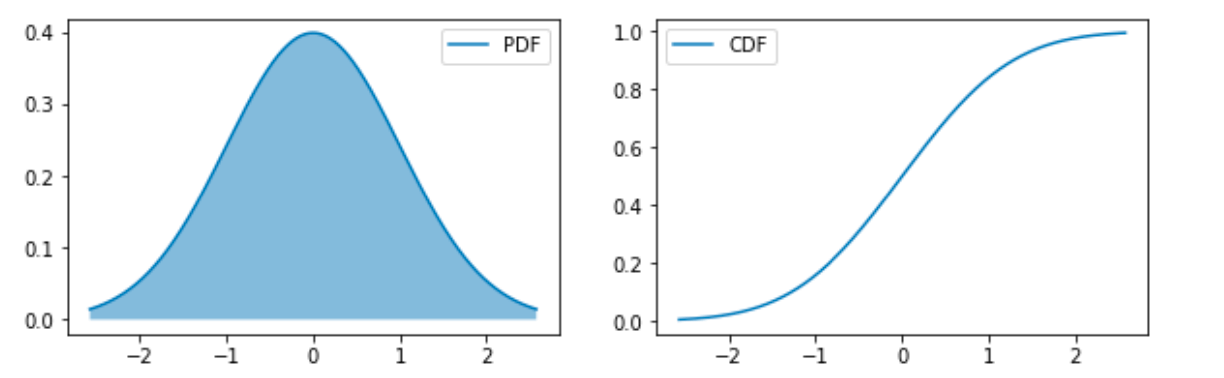
高斯分布 (Gaussian Distribution) 或正态分布 (Normal Distribution) 形式如下:
有时也会用 表示分布的精度 (precision)。中心极限定理 (Central Limit Theorem) 认为, 大量的独立随机变量的和近似于一个正态分布, 因此可以认为噪声是属于正态分布的。
from scipy.stats import nrom
fig, axes = plt.subplots(1,2,figsize=(10,3))
mu, sigma = 0,1
X = norm(mu,sigma)
plot_distribution(X,axes=axes)
tip
什么时候采用正态分布?
在缺乏分布的先验知识,不知道选择何种形式,默认选择正态分布总不会出错的,因为:
- 中心极限定理告诉我们,很多独立随机变量都近似服从正态分布,现实中很多复杂系统都可以被建模成正态分布的噪声,即使该系统可以被结构化分解
- 正态分布是具有相同方差的所有概率分布中,不确定性最大的分布,换句话说,正在分布对模型加入的先验知识最少的分布。
指数分布
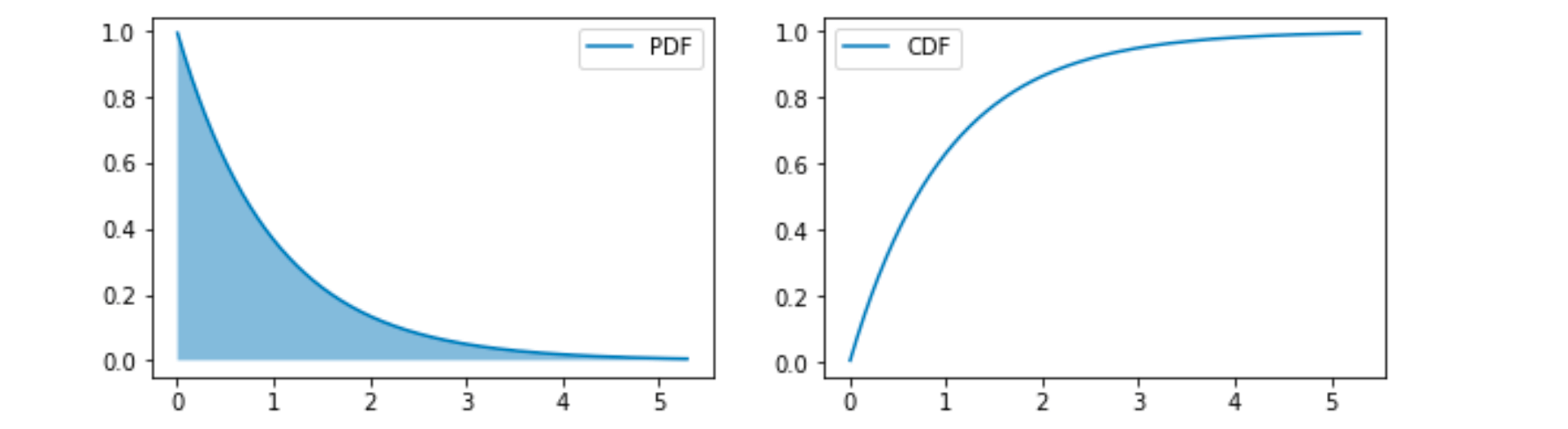
指数分布 (Exponential Distribution) 形式如下:
其中 是分布的一个参数, 常被称为率参数 (Rate Parameter);
tip
指数分布有什么特点?
在 处获得最高的概率
拉普拉斯分布
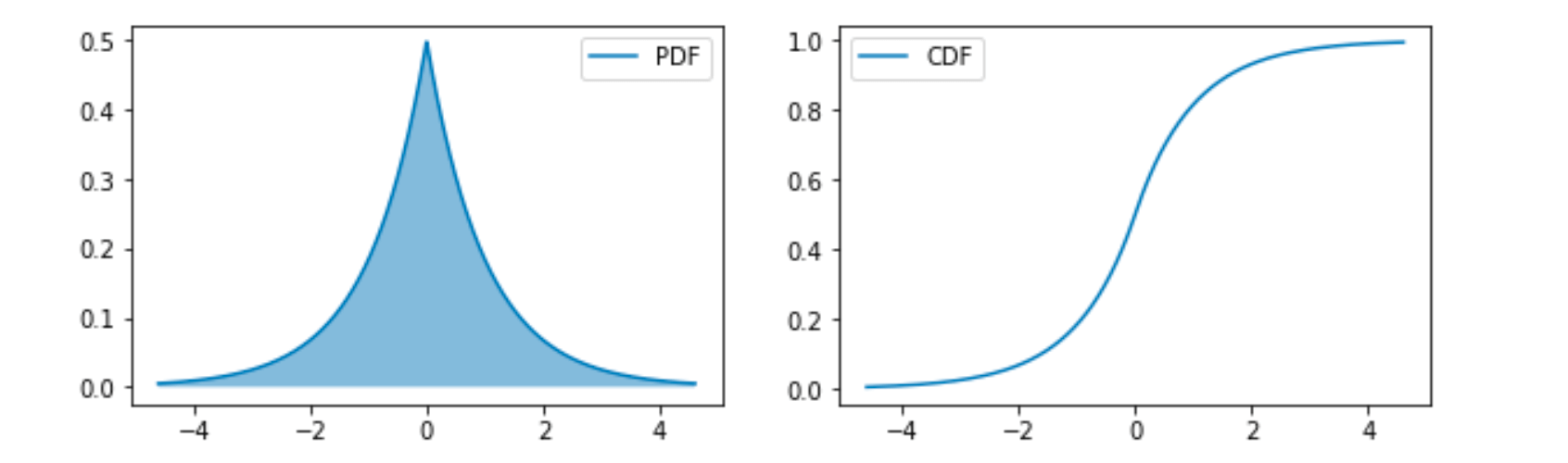
拉普拉斯分布(Laplace Distribution)形式如下:
这也是可以在一个点获得比较高的概率的分布。
一些概率论面试问题
1、变量与随机变量有什么区别?
2、随机变量与概率分布有什么联系?
3、联合概率与边缘概率有什么区别?有什么联系?
4、常见的概率分布有哪些?有什么应用场景?请举例说明
5、大数定律和中心极限定理的意义与作用(切比雪夫大数定律)
6、正态分布的和还是正态分布吗,正态分布性质与独立同分布)★
7、什么是假设和检验?
8、数学期望和方差?
9、独立和不相关的区别?
10、概率密度函数?
11、举几个泊松分布的例子
12、说一下全概率公式和贝叶斯公式 ★
13、解释下相关系数、协方差、相关系数或协方差为0的时候能否说明两个分布无关?
14、若干正态分布相加、相乘后得到的分布分别是什么?
15、假如有一枚不均匀的硬币,抛正面的几率是p,抛反面是1-p,请问如何做才能得出1/2?★
16、机器学习为什么要使用概率?
参考
[1][https://github.com/MingchaoZhu/DeepLearning](https://github.com/MingchaoZhu/DeepLearning)