什么是 Normalizing Flows
Generator
Generator是一个网络,这个网络定义了一个概率分布 pG。 给生成器一个输入(比如一个正态分布的输入z),生成器就会生成一个概率分布 pG(x),x=G(x)。我们希望让生成的概率分布pG(x)和数据的分布pdata(x)尽可能的相似。
假设现在我们有很多的样本 {x1,x2,…,xm} from Pdata (x) ,那么Generator的优化目标就是:
G∗=argGmaxi=1∑mlogPG(xi)≈argGminKL(Pdata∥PG) Flow-based model 非常厉害的地方就在于,它可以直接去优化这个目标函数。VAE和GAN都不能直接去优化这个函数。
数学基础
Jacobian矩阵
令 z=[z1z2], 现在我们有一个方程 x=f(z), x=[x1x2] (x和z的维度可以不一样)。那么f这个函数的Jacobian矩阵就可以如下定义(注意是f这个函数的Jacobian矩阵)
Jf=[∂x1/∂z1∂x2/∂z1∂x1/∂z2∂x2/∂z2] Jacobian矩阵还有一个性质就是 Jf 和 Jf−1 互为 inverse。
行列式(Determinant)
行列式是一个标量,感觉类似于矩阵的大小信息。这个是线性代数的基础知识了。比如我们有一个矩阵 A=[acbd], 那么它的行列式就是 det(A)=ad−cb。同样的3x3的行列式也有对应的计算公式。
还需要知道的一个比较重要的性质就是下面的公式:
det(A)=1/det(A−1)det(Jf)=1/det(Jf−1) 行列式的实际含义就是:行列式矩阵就是高维空间中体积的概念, 如下图所示:

Change of Variable Theorem
Change of Variable Theorem的主要思想就是求两个分布直接的变换关系。
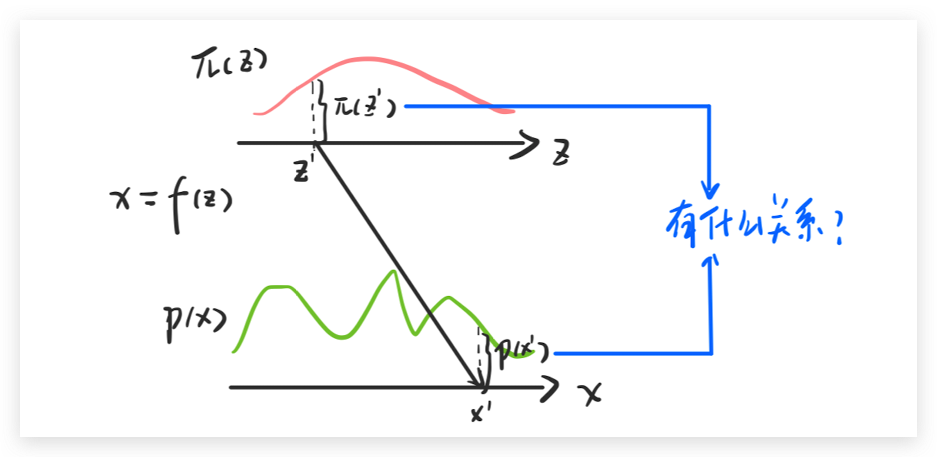
我们先看一个简单的方程,先假设我们有一个分布 π(z), 这个分布在0-1之间的值都是1,也就是说 ∫π(z)dz=1 。假设x和z之间的关系是 x=f(z)=2z+1。那么也就有 p(x0′)=21π(z′)。
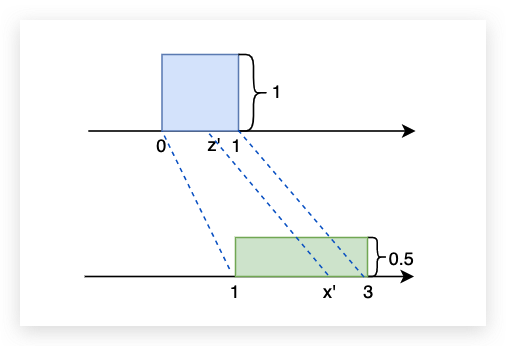
下面我们看一个更加一般的例子,假设上面的z和x的分布都是无规律的。我们还可以写出z和x之间的变化规律吗?答案是可以的。这里用到了一个极限的概念,下面用李宏毅老师课上的PPT来进行解答(当Δx足够小的时候就可以将不规则曲线看做是面积,于是就有了PPT上的公式推导)。
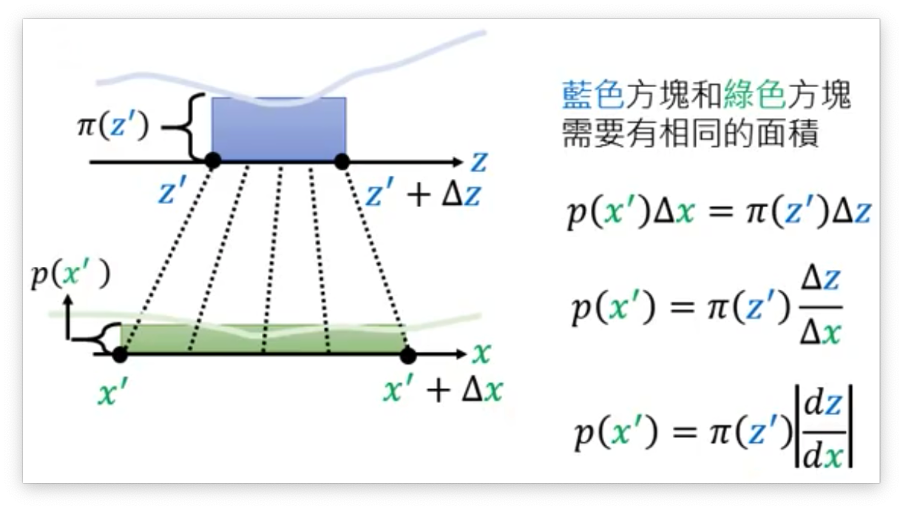
上面说的是一维的情况,对于二维的情况我们也可以用类似的极限思想得到如下的公式:
p(x′)∣∣det[Δx11Δx12Δx21Δx22]∣∣=π(z′)Δz1Δz2 下面我们对上式进行一定的推导,推导过程如下就可以得到最终的结果:
p(x′)∣∣det[Δx11Δx12Δx21Δx22]∣∣=π(z′)Δz1Δz2x=f(z)p(x′)∣∣Δz1Δz21det[Δx11Δx12Δx21Δx22]∣∣=π(z′)p(x′)∣∣det[Δx11/Δz1Δx12/Δz2Δx21/Δz1Δx22/Δz2]∣∣=π(z′)p(x′)∣∣det[∂x1/∂z1∂x1/∂z2∂x2/∂z1∂x2/∂z2]∣∣=π(z′)p(x′)∣∣det[∂x1/∂z1∂x2/∂z1∂x1/∂z2∂x2/∂z2]∣∣=π(z′)p(x′)∣det(Jf)∣=π(z′)p(x′)=π(z′)∣∣det(Jf)1∣∣ 所以最后我们就可以发现,p(x) 可以有 z(x) 除以 f 的 Jacobian矩阵的行列式的绝对值得到。
Flowed-based Model
好的下面我们首先回头看Generator的优化目标:
G∗=argGmaxi=1∑mlogpG(xi) 现在我们知道了:
pG(xi)=π(zi)∣det∘(JG−1)∣Zi=G−1(xi) 带入到Generator的优化目标中可得:
log(xi)=logπ(G−1(xi))+log∣det(JG−1)∣ 一切看起来很美好,但是计算上面的式子也是需要一定的条件的:
- 你需要能够计算JG
- 你的 G 必须是可逆的才行
上面的两个现在条件就决定了 G 的结构一定不能很复杂,为了优化Flow-based 模型的表达能力。所以Flow-based的模型就是使用了很多 G 组合起来,这样就是为什么要叫做Flow的原因。
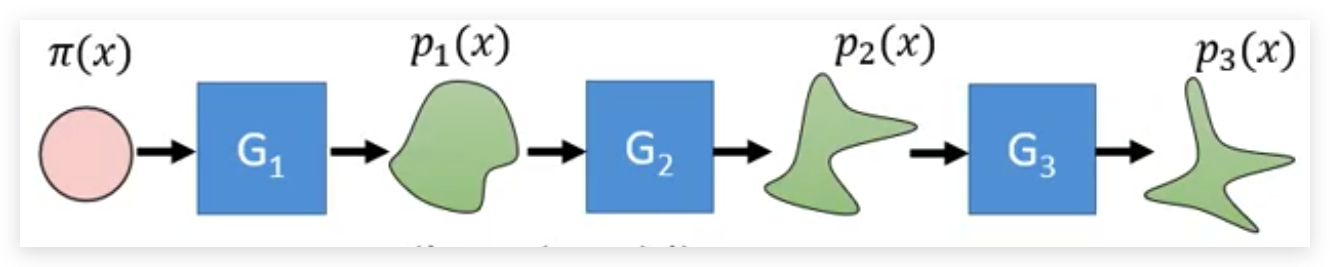
如何训练
虽然我们有很多个Gi作为生成器,但是其实我们在进行训练的时候只需要把所有的Gi都看做一个大的G。 对于一个图像生成的任务来说,我们一般都是训练 G−1 把它训练好了之后反过来就可以用作图像生成了。
Coupling Layer
前面已经说到了,我们的G需要有一定的限制,首先它要方便去计算Jacobian矩阵,然后它还需要是可逆的,Coupling Layer就是满足这样条件的Generator。它的结构就如下所示:
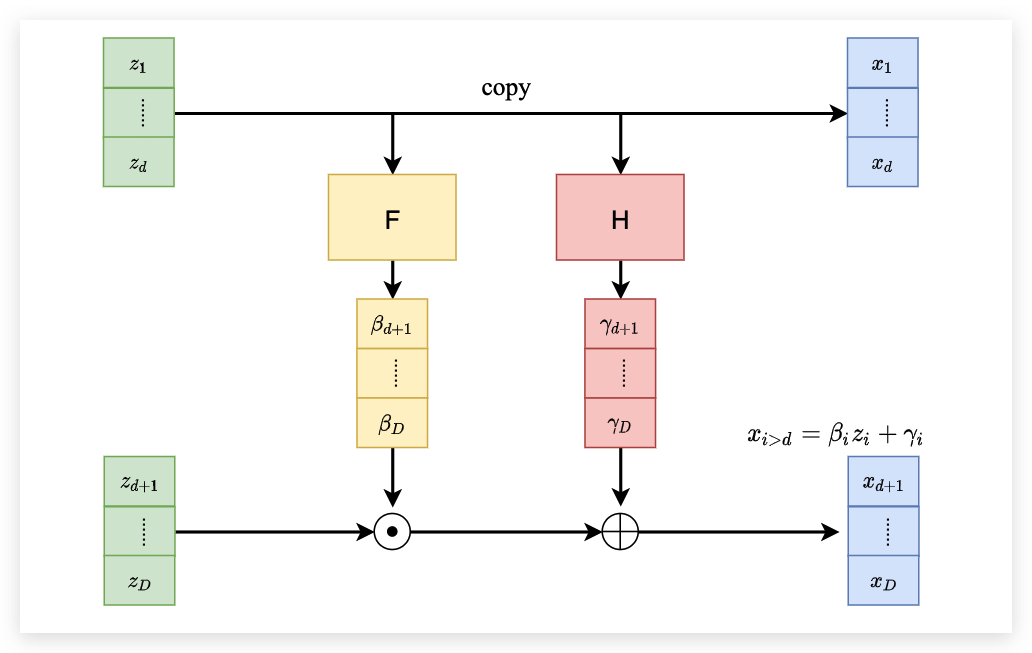
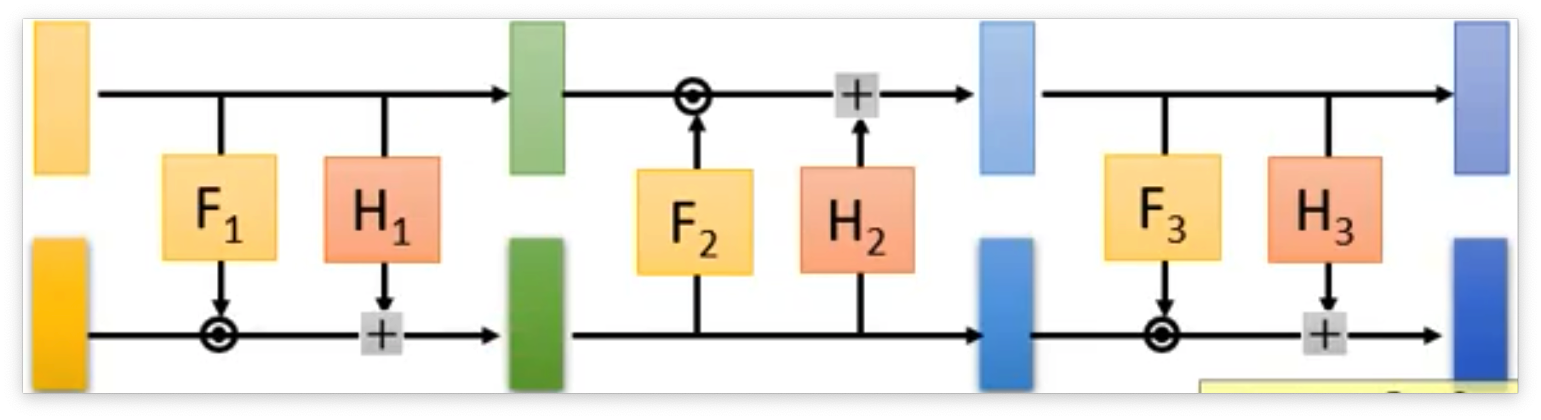
首先将输入分为两个部分,第一个部分直接不动的移动到右边。同时上面的部分会经过一个F函数和一个H函数,分别和下面的部分进行点积和点加后作为下面右边的部分。 下面来看一看这个矩阵是如何计算Jacobian矩阵的和为什么可逆。
首先看一下为什么是可逆的,现在我们需要通过 x 求解 z 那么可以发现 z1 到 zd 的部分就等于 x1 到 xd。有了 z1 到 zd 之后我们就可以直接计算出 β 和 γ 。 那么后面将 xd+1 到 xD 减去 γ 之后再除以 γ 就可以得到 zd+1 到 zD 了。 这样我们就完成了网络逆向的过程。
Coupling Layer的Jacobian计算可以用下面的一张图来说明:
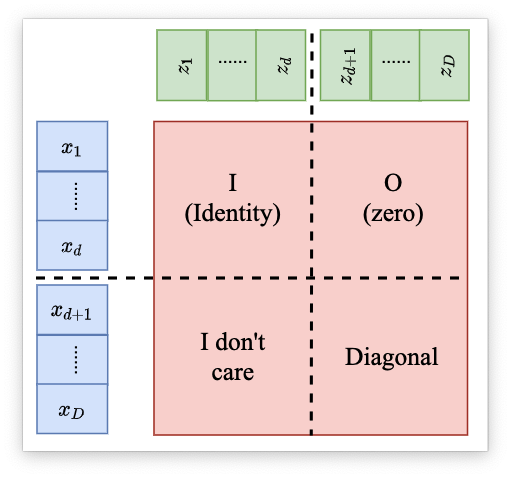
可以发现 Jacobian 矩阵的行列式只与右下角的有关。右下角的 Jacobian矩阵 经过计算之后可以发现是一个对角矩阵。其他部分的导数都为0,所以是一个对角矩阵。那么这个矩阵的Jacobian的计算公式就如下:
det(JG)=∂zd+1∂xd+1∂zd+2∂xd+2⋯∂zD∂xD 把 Coupling Layer 叠加起来就可以获得一个完整的Generator:
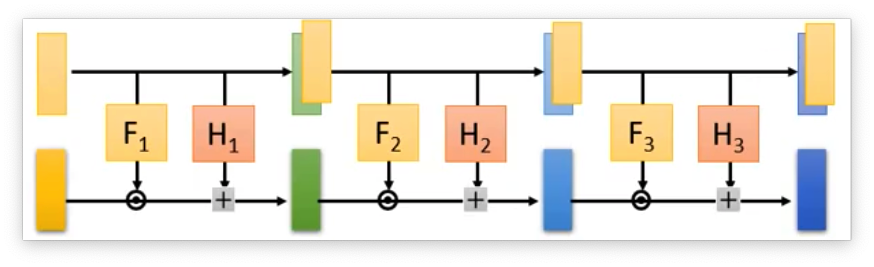
但是在叠加的时候需要用一些手段,因为我们可以发现如果直接叠加的话,那么上面部分一直是不变的,从直觉上就感觉很不好。 所以在叠加的时候,就将Coupling Layer反向叠加起来。
到这里经典的flow思想就已经介绍完了,其他还有一些经典的flow模型看后面再去介绍









