Skip to main content

神经网络与反向传播

上一节课中已经学习了如何定义损失函数以及根据这个损失函数去分类器。在这节课中将会学习神经网络与反向传播。

神经网络​

在上节课的内容中介绍了线性分类器，最简单的神经网络结构其实就是在线性分类器之后添加了激活函数。然后通过堆叠的方式形成了多层的结构。

其中的 max(0,W1x)max(0,W_1x) 就是一种激活函数，也是一种非常经典的激活函数叫做 RELURELU 激活函数。

一个最简单的二层神经网络模型如下：

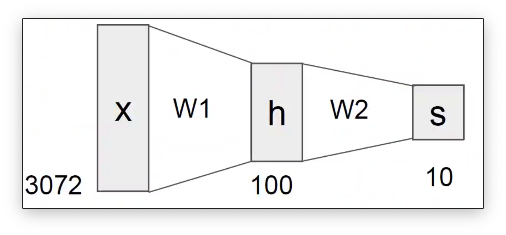
“神经网络”是一个非常广泛的术语。对于上述的模型我们可以用全连接网络或者多层感知器(MLP)来描述他。

如果我们不用激活函数，得到的结果会更好吗？

如果我们不用激活函数，以两层的网络结构举例。

f=W2W1xW3=W2W1∈RC×H,f=W3xf=W_{2} W_{1} x \quad W_{3}=W_{2} W_{1} \in \mathbb{R}^{C \times H}, f=W_{3} x \\

堆叠的结果可以写成f=W2W1xf=W_2W_1x堆叠的结果又可以简写为 f=W3xf=W_3x ，这样的话其实就和单个的线性层没有任何的差别了。

非线性激活函数为神经网络带来了非线性，否则堆多少层神经元都与单个线性层无异。激活函数为神经网络提供的非线性让神经网络能够拟合非线性边界。

常见的激活函数​

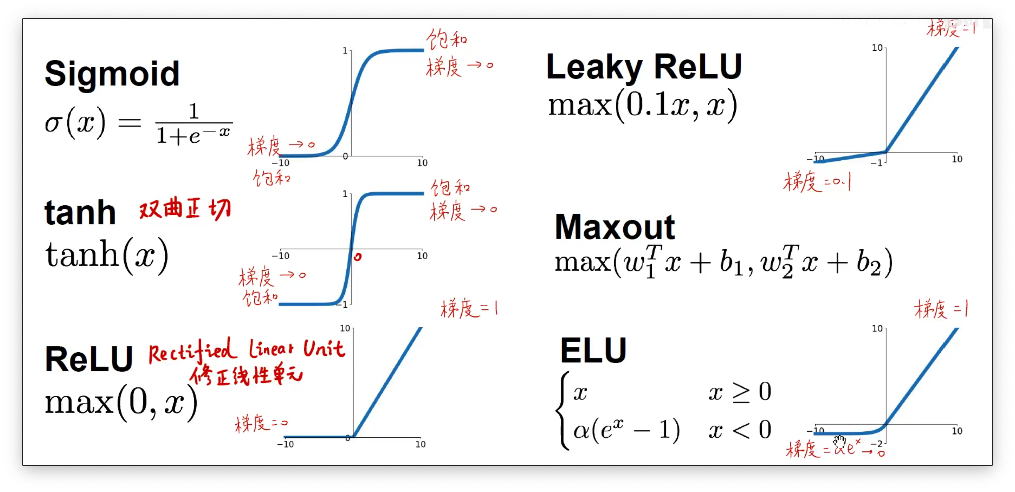
下图展示了常见的一些激活函数，目前使用的最广泛的就是Sigmoid和ReLU激活函数。

神经网络的结构​

一个最基础的神经网络包含了输入层，隐藏层和输出层三个结构。

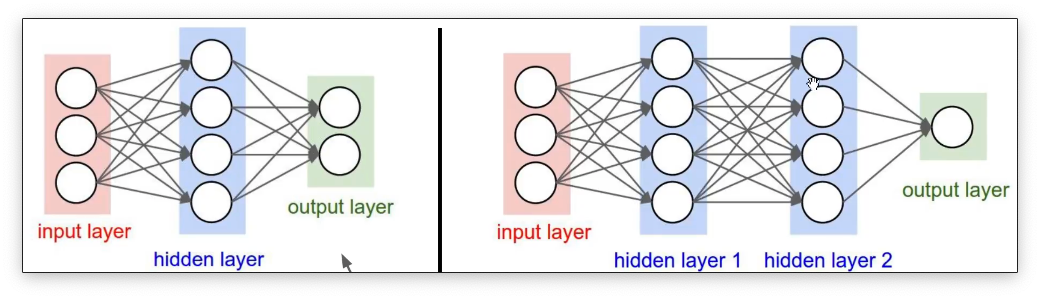
输出层的神经元个数可以有非常多的含义，比如对于一个分类网络来说，输出层的神经个数往往就代表了类别个数。上图中的神经网络都是一个一个连接的，这一类的神经网络叫做 “全连接神经网络”

全连接网络的numpy代码实现：

import numpy as np
from numpy.random import randn

N,D-in,H,D_out = 64,1000,100,10
x,y = randn(N, D_in), randn(N, D_out)
w1, w2 = randn(D_in, H), randn(H, D_out)

for t in range(2000):
    h = 1 / (1 + np.exp(-x.dot(w1)))
    y_pred = h.dot(w2)
    # 计算平方差loss
        loss = np.square(y_pred-y).sum()
    print(t, loss)
    
    # 返现传播计算
    grad_y_pred = 2.0 * (y_pred - y)
    gred_w2 = h.T.dot(grad_y_pred)
    grad_h = grad_y_pred.dot(w2.T)
    grad_w1 = x.T.dot(grad_h * h * (1 - h))
    
    # 更新权重参数
    w1 -= 1e-4 * grad_w1
    w2 -= 1e-4 * grad_w2

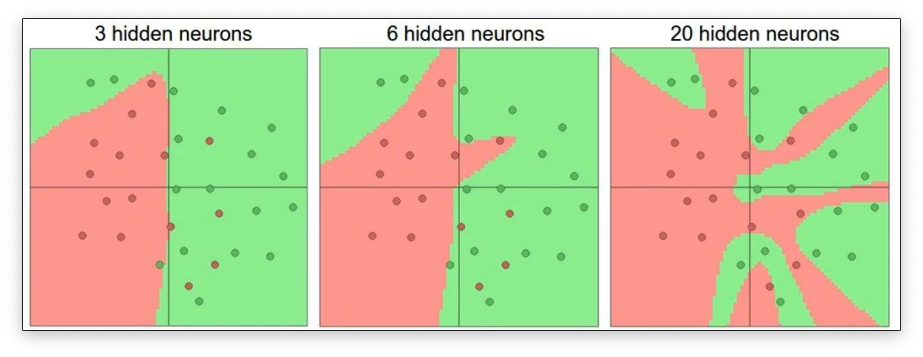
正是由于神经网络的非线性，他才可以捕捉到非常底层非常高级的一些特征。比如对于下面的分类问题，神经网络就可以完全拟合数据的分布：

反向传播

我们已经知道了，神经网络是通过求导数的方式来进行权重参数的更新。但是目前的神经网络的层数非常的大，我们没有办法很轻易地用一个数学公式来表示神经网络。层数非常多也表明了我们需要求导的 “公式” 非常的复杂。在数学上我们是采用链式求导的方式来进行神经网路的梯度更新。进行梯度更新的过程我们把它叫做神经网络的反向传播。

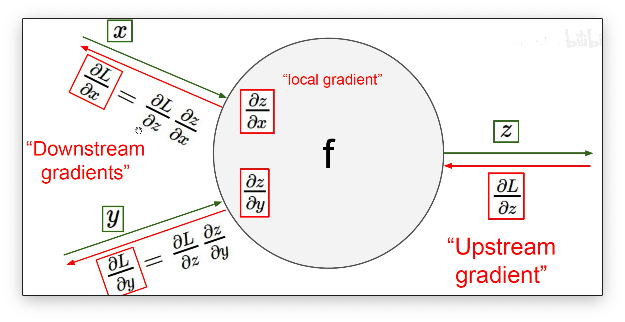
让我们对一个复杂的神经网络手动计算反向传播的过程基本上是不可能的。但是当今在各大深度学习框架的加持下求神经网络的偏导数其实是一件非常简单的事情。本节的视频课中其实对于反向传播的运算过程进行了非常详细的讲解，但是计算的过程并不容易用文字的形式记录下来，这里我就没有写了。

在本节课中我们学习了神经网络的基础知识，了解了神经网络参数的更新过程。本节课的内容为下一节课中的卷积神经网络提供了一个基础。